As more opportunities arise in the world around us, it becomes increasingly complex. We often find ourselves so overwhelmed by the growing influx of information that we try to avoid complexity. At the same time, for many people, one of the most enjoyable experiences is when something completely incomprehensible just a second ago suddenly becomes clear. Drawing on scientific research, the concept of emptiness in Buddhism, and observations of the infinite diversity of the world, we will dive into the beauty of complexity using thought-provoking analogies. By examining its role in our lives and its influence on our understanding of the universe, we can better recognize the deep interconnectedness of the world around us. And I will try to write about complexity simply.
Definitions
This isn’t a scientific article, but it does touch on science in one way or another. So, like true scientists, let’s begin with definitions. If we skip this step, we might find ourselves with differing understandings of key concepts, which are the foundation upon which everything rests. At the same time, I can’t be entirely precise with my definitions to avoid delving into formulas and mathematics. I will strive to strike a balance between common knowledge and accurate phrasing.
Entropy
What do scientists do? In reality, they engage in the same activities as any other living beings. Scientists seek to understand the laws that govern the world to predict the future. Why do we need to predict the future? To minimize losses from unexpected surprises and maximize the resources available to us. Nobody enjoys loss or need. The world, however, is chaotic and unpredictable.
Entropy is the opposite of predictability. We can view the evolution of living beings as a struggle against entropy. For example, ancient arthropods called trilobites developed eyes composed of multiple-faceted lenses through evolution, allowing them to better navigate their marine environment, actively search for food, and evade predators. This increased the trilobites' survival rate and allowed them to dominate marine ecosystems for an extended period. Thus, individuals without eyes did not survive, while those with eyes reproduced and passed on their discovery to offspring, who similarly improved upon it. Random mutations leading to the development of eyes were preserved, while individuals lacking such mutations were eliminated.
Evolution is a lengthy process. Humans combat entropy by creating and accumulating knowledge. This is a much faster process, as it doesn’t require waiting for the long turnover of generations, but it is generally similar to the evolution of living beings. People propose theories about how the world works and then test how accurately they predict the future. Those theories that make poor predictions are either discarded or modified to make better predictions. In this way, theories evolve, and entropy is reduced.
Information and Complexity
You take socks out of the washing machine. What’s faster - sorting them and pairing them in a drawer, or stuffing them unsorted and searching for a matching sock each time? From a time-saving perspective in the mornings, the first option is preferable. However, in terms of complexity, there is no difference. You can sort them all at once, spending a lot of time, or perform the sorting step once a day, spending a little time each day. The number of operations is the same, and the complexity is the same.
We see that to overcome the entropy created by the washing machine, certain actions need to be taken.
What do scientists do to overcome the entropy of a phenomenon they don’t understand and thus cannot predict? They perform actions in the form of acquiring information.
Scientists typically study the interactions between certain entities. The collection of interacting entities is called a system. In our case, these are socks looking for their pair. Since almost everything we encounter in the universe can be broken down into parts, the whole universe consists of systems and interactions.
Information is what allows us to reduce uncertainty in a system. One could say that information is the reduction of a system’s entropy. The more information, the less entropy.
Complexity is a measure of how difficult it is to understand or define a system. The more complex a system, the more information is required to describe or understand it. If all your socks are identical, sorting them will take very little time. Any two socks make a pair. If, like me, you have multi-colored socks, sorting them is considerably more difficult. On the bright side, I can convey much more information to the world by wearing cheerful or sad socks, depending on my mood.
Thus, entropy, information, and complexity are interconnected. Entropy and complexity are related because complex systems generally have higher entropy. Information reduces entropy and simplifies complexity, making the system more understandable and organized.
Ways to combat complexity
Great, we’ve sorted out the terminology. Now let’s move on to the most interesting part. In the process of overcoming entropy, one has to overcome complexity. The evolution of life and the evolution of human knowledge have found many ways to combat it.
Divide and conquer structure
When you first start learning a foreign language, everything may seem complicated and incomprehensible. You hear a native speaker’s speech, and for you, it’s just a stream of sounds.
However, if you study the language in parts, taking it step by step, you will soon notice progress. You start with basics like the alphabet and phonetics, then gradually move on to studying grammar, expanding your vocabulary, and improving your communication skills. As a result, by breaking down this complex process into small and understandable parts, you begin to comprehend the foreign language and eventually can communicate freely in it. Now you can easily pick out words and sentences from the stream of sounds. You can’t believe you once didn’t understand this language!
The steps of learning are interconnected. Without knowing the alphabet, it’s hardly worth tackling grammar. Each step is broken down into smaller ones.
In general, one could say that we strive to structure information. For example, this post has some structure. It has headings and subheadings. We started with simple terms and are now delving into examples.
In general, this method of cognition was well described by Rene Descartes in 1637: "to divide all the difficulties under examination into as many parts as possible, and as many as were required to solve them in the best way" and "to conduct my thoughts in a given order, beginning with the simplest and most easily understood objects, and gradually ascending, as it were step by step, to the knowledge of the most complex; and positing an order even on those which do not have a natural order of precedence."
And this method worked so well that at some point, scientists felt they had already practically studied everything. Here are a few quotes:
Albert A. Michelson: "It seems probable that most of the grand underlying principles have been firmly established and that further advances are to be sought chiefly in the rigorous application of these principles to all the phenomena which come under our notice. It is here that the science of measurement shows its importance — where quantitative work is more to be desired than qualitative work. An eminent physicist remarked that the future truths of physical science are to be looked for in the sixth place of decimals." (1894, the dedication of Ryerson Physical Laboratory, quoted in Annual Register 1896)
Hendrik Antoon Lorentz: "According to our present views, all fundamental laws of nature have been discovered and tested. Existing experiments do not indicate that any further new principles will be discovered. Hence, we may say that the laws of nature in their final shape are known, and that the discovery of new relations within them, as well as deviations from them which still need to be accurately determined, are the only tasks which still await the physicist. The exploration of these tasks will inevitably lead to a deeper insight into the foundations of physics." (Lorentz, H.A. "The Present Status of Radiation Problems." Nobel Lecture, 1902)
Literally soon after, Einstein published his theory of relativity and quantum mechanics emerged. The world, which seemed so understandable and predictable, revealed to scientists how much hidden entropy it still contained. To this day, they are trying to develop a coherent and non-contradictory theory that unifies all these discoveries.
It seems that we cannot simply break down something complex into small parts and hope that they will eventually form a complete picture.
Emergence
Imagine yourself as a scientist studying red imported fire ants. You analyze their behavior, anatomy, and social structure. Ants have certain properties, such as living in colonies, having a division of labor between workers, soldiers, and the queen. Their action program seems simple: search for food, care for offspring, and protect the nest. By studying their individual characteristics, you might think you already know everything about them and can predict their behavior in various situations. Your predictions even work well.
But then a flood comes, and you think they will all die because their simple action program does not provide for adaptation to such conditions. However, instead of perishing, they come together and form a new structure that does not follow from their simple properties. This structure is called a "living raft". Here’s what it looks like:

The living raft is a construction made of ants that connect themselves to one another using their legs and bodies, forming a floating platform capable of holding the entire colony above water. This phenomenon is an example of emergence, where new properties and qualities arise from the interaction of simple components. In this case, the simple properties and behavior of individual ants would not predict the emergence of such a complex adaptive structure as a living raft.
Emergence is that surprising moment when, after studying each individual component of a system, you think you understand the entire system as a whole. If you look around, you’ll most likely see the fruits of the labor of millions of people - houses, cars, the internet, satellites, and airplanes flying overhead. It’s hard to believe that an upright-walking primate, which runs slowly, has small fangs, and weak muscles, could build all of this. This is an example of unity and collaboration, as well as the battle between emergence and entropy.
Lossless Compression
Every time I see Romanesco broccoli in a store, I can’t help but stare at it for a long time.
.jpg)
It’s mesmerizing to admire its beauty endlessly. This shape is quite complex, unlike a simple sphere (like a watermelon) or a parallelepiped (like a milk carton). But how much information is needed to explain its structure? Is it really more complex than a watermelon?
Today, while on a walk, I photographed a tree. Take a look at any branch that extends from the trunk. It appears to be a miniature version of the tree itself.

Leonardo da Vinci, in his notes, wrote: "All the branches of a tree at every stage of its height when put together are equal in thickness to the trunk [below them]".
Now let’s compare the photo of the tree with a photo of Long Island, Bahamas.

In the same notes, Leonardo continued: "All the branches of a water [course] at every stage of its course, if they are of equal rapidity, are equal to the body of the main stream."
Surprisingly, these ideas didn’t receive much development until the mid-20th century, and such objects didn’t even have a name. Mathematician Benoît Mandelbrot noticed and began studying them. He called his discovery fractals. A fractal is a geometric object that possesses the property of self-similarity, meaning its parts replicate the shape of the whole object at different levels of scale. Fractals are often used to describe complex forms that cannot be represented by simple geometric shapes, such as lines, circles, or rectangles. Once you see fractals, you’ll start noticing them everywhere. Tree branches and lightning, snowflakes and frost on the window, river deltas and human lungs, mountain ranges and clouds.
I wrote a small program that constructs a tree. Let’s run it to understand how fractals emerge.
Click the "Start" button below to see this algorithm in action.
This isn’t an animation; it’s actual JavaScript code. It implements a function that draws a branch with a specified angle and length from a starting point with given initial coordinates (startX, startY). Then it calls itself twice for each of the two new branches, reducing the branch length by 30% and changing the branching angle by 30 degrees. As the starting point for the new branches (startX, startY), the endpoint of the current branch is passed (determined by its initial coordinates, branch length, and angle of inclination). The process repeats for each branch. This process, where a function calls itself, is called recursion.
So, with just one function, we can describe the entire tree. We don’t need to calculate the coordinates and inclination of all branches beforehand; each branch draws itself. It doesn’t know and doesn’t need to know anything about the whole tree. It has a function that drew it and calls this function to draw two more branches similar to it but smaller in size and with a different angle of inclination. Since the new branches are a scaled-down copy of the current branch, all the information (initial coordinates, inclination, branch length) is available at each step.
To understand how a fractal structure works, we need to understand how this single step works. And that’s it. What looks very complex becomes very simple.
The same system can be described differently, creating different amounts of information and, therefore, usually different complexity. A tree can be described in great detail, or it can be described as the first step and recursion. You compress information without losing its ability to describe the system, making the system more understandable. The first conclusion is that complexity is not only about the system itself; complexity depends on the person comprehending the system because it matters how they do it.
As I said, once you understand what a fractal is, you’ll see them everywhere. If you look around, you’ll see tree-like structures at every turn. In organizations, there are CEOs, their deputies, deputies of deputies, and so on.
River systems, blood vessels, and electrical networks share a tree-like structure. The evolution of anything can be represented as a tree, with each branch being a path from one mutation to another. Why is it so prevalent? Recursive structures have advantages like resource efficiency. They enable optimal use of space and materials by providing the maximum surface area with minimal material.
These structures also offer adaptability and flexibility. They allow systems to adjust to changing conditions. For example, river branching finds the path of least resistance, while tree branching optimizes sunlight absorption for photosynthesis.
As we have already noted, another example of using a tree-like structure is the post you are reading. Here we have headings and subheadings. Tree-like structures are often used to organize knowledge. Why do we do this? It can be an interesting food for thought.
Abstraction
You might argue that real trees don’t look as uniform as the ones created by our recursive algorithm, and you would be right. Indeed, we have neglected some details. Scientists often do this. Instead of studying reality in all its intricacies, they construct a model that, to some extent, reflects certain properties of reality. This may sound unreliable. What if we overlook crucial details? It could happen, but we don’t know in advance what’s essential and what’s not. With so many details, we must disregard some of them. That’s why we build a model and evaluate how well it reflects reality. If reality surprises us, it means our model doesn’t account for those important details.
What does an abstraction like a fractal offer us? By neglecting details, we discover that trees, shrubs, rivers, circulatory systems, and organizations all share the same structure. This suggests that by understanding this structure, we can gain insights into many aspects of reality that function similarly.
Abstraction is the process of simplifying or generalizing complex objects, situations, or concepts, allowing us to focus on essential characteristics and filter out insignificant details. You don’t need to know the inner workings of a car to drive it. Even details such as whether it runs on gasoline or electricity can be disregarded until it’s time to refuel. We apply abstraction everywhere.
Essentially, language is also an abstraction. Each object, in reality, corresponds to one or more words in a language. However, words evoke different images for different people. If I say "table," you won’t imagine the exact same table as I do. We compress reality and then decompress it with some loss. In this way, we express one abstraction using another, striving to find a balance between simplification and accuracy.
Game of Life
To better understand complexity and how it can be modeled, let’s look at a famous model called "The Game of Life." It was invented by English mathematician John Conway in 1970.
On a two-dimensional grid, each cell can be in one of two states: "alive" or "dead." The transition between states depends on the state of neighboring cells.
The rules of the Game of Life are simple and based on the following principles:
-
Survival. Each cell with two or three neighboring live cells survives.
-
Death. Each cell with more than three live neighbors dies due to overpopulation. Each cell surrounded by empty neighboring cells or only one occupied cell dies from loneliness.
-
Birth. If the number of live cells bordering an empty cell is exactly three (no more and no less), a new "organism" is born, meaning the cell becomes alive in the next move.
It is essential to understand that the birth and death of all "organisms" occur simultaneously. Together, they form one generation or one move in the evolution of the initial configuration.
The Game of Life has no specific goal and is not a game in the usual sense of the word. It is more of a mathematical model used to study the dynamics of systems and self-organizing processes. Depending on the initial configuration of cells, the Game of Life can lead to various outcomes: stable structures, oscillating patterns, or chaotic formations.
Try to guess what will happen on the grid, then press the Start button to check your guess.
The middle cell always has two neighbors and survives according to rule 1. Live cells that share sides with the middle cell die due to loneliness (rule 2), while dead cells are revived thanks to three neighbors (rule 3), causing the figure to switch between horizontal and vertical states. We get a blinking figure. Conway called it a Blinker.
Add one more cell, and we’ll get a completely different picture.
The oscillations have disappeared. The population is stable.
In the following example, the population of cells disappears completely in just a few steps.
But change just one cell, turning an "H" into a "П", and the situation changes in a completely unpredictable way.
Just one cell in a new position, and instead of death, there is a very lively life, which after many iterations brings the population to a stable state. If this surprised you, then you have experienced the sensations that researchers feel when they encounter emergent states.
Very simple rules lead to very complex behavior, which is impossible to predict, because often the number of involved cells grows so fast that it goes beyond human capabilities, and sometimes beyond existing computing power.
It turns out that the Game of Life is perfect for modeling processes occurring in reality. The spread of fires, rumors, epidemics, cancer cells, corrosion in metals, traffic jams on roads, self-organization of patterns in nature (e.g., patterns on mollusk shells and butterfly wings) and in societies, modeling climate change and temperature anomalies, and urban infrastructure development.
New and interesting patterns were found. Here, for example, is a Glider:

A pattern that, after several steps, reproduces itself, but in a new place, and thus moves across the field.
In all the experiments John Conway observed, cell populations either completely vanished or stabilized without further changes. There is also the Rule 2, according to which cells die due to overpopulation. Based on this, he hypothesized that the number of alive cells is always limited. Conway believed that the number of alive cells could not grow indefinitely. He even offered a prize to anyone who could disprove his hypothesis. Soon he paid the prize. A group from MIT came up with a gun that shoots gliders (Gospers glider gun).
Since the number of gliders coming out of the gun is infinite, the number of cells will also grow infinitely.
It’s very convenient when theories can be built and refuted in such a visual way.
And you may have noticed that we think less and less in terms of cells and more and more in terms of patterns in which cells are arranged. From the level of cell interaction, we have risen to a new level of abstraction - the interaction of patterns.
I can’t help but delve a bit deeper into this topic. For those not familiar with programming or mathematics, it may seem somewhat complex or overly abstract. In that case, feel free to skip ahead to the next section, Infinite games.
Moving from the cellular level to the level of patterns, we notice that Gosper’s Glider Gun, by shooting gliders, can transmit information from one part of the field to another. Colliding, gliders neutralize each other, so the signal can be "turned off".
A cell is a static on-off state. Gosper’s gun allows us to transmit these on-off states at a distance.
If you look closely at the Game of Life, you can see its similarity to a computer. In a computer, all information is stored as bits, which can be either 0 or 1, just as a cell can be filled or not. A group of bits can be interpreted in many different ways. For example, if the position of each bit is a power of 2, then a group of three bits, 101, can be interpreted as the number 5 (since 1×22 + 0×21 + 1×20 ), and any number can be represented this way (in fact, this is how numbers are represented in your computer). Using Gosper’s guns, you can perform logical operations in the Game of Life. From logical operations, you can build chains and create any programs. For example, a calculator that performs calculations on numbers encoded in cells. Thus, a game based on three simple rules turns into a computing machine on which you can program anything you want. This is yet another example of emergence.
Infinite games
In 2006, the pattern OTCA metapixel was published. It occupies 2048x2048 cells and is a meta-cell. That is, it is a cell made up of cells.
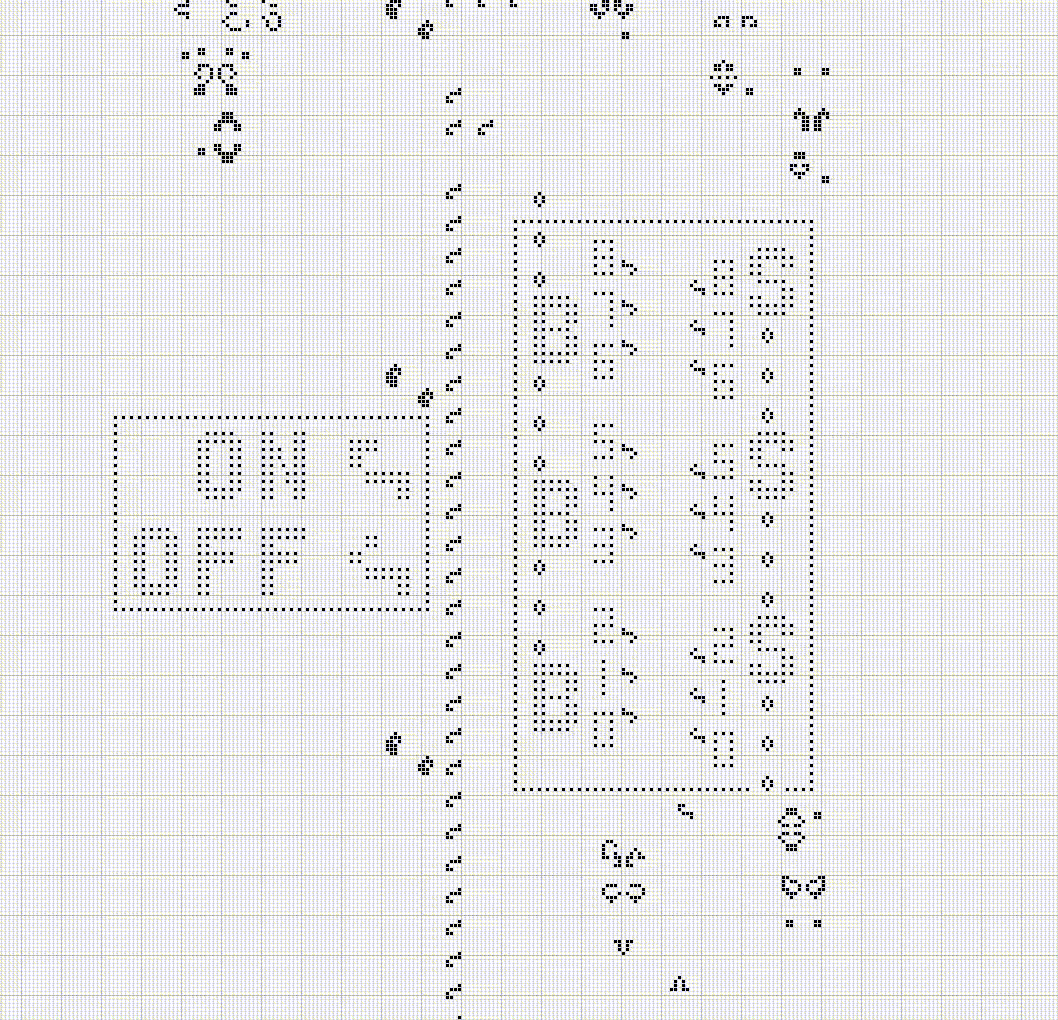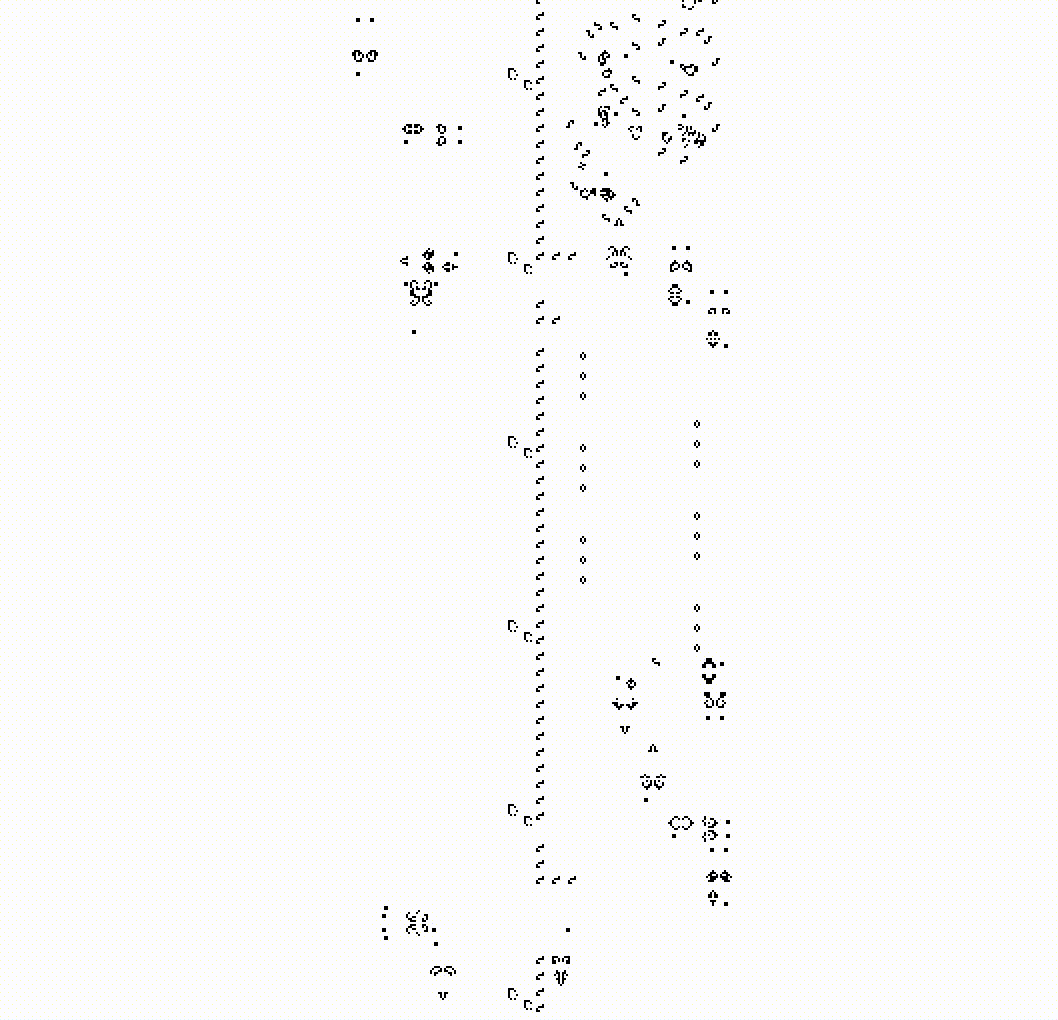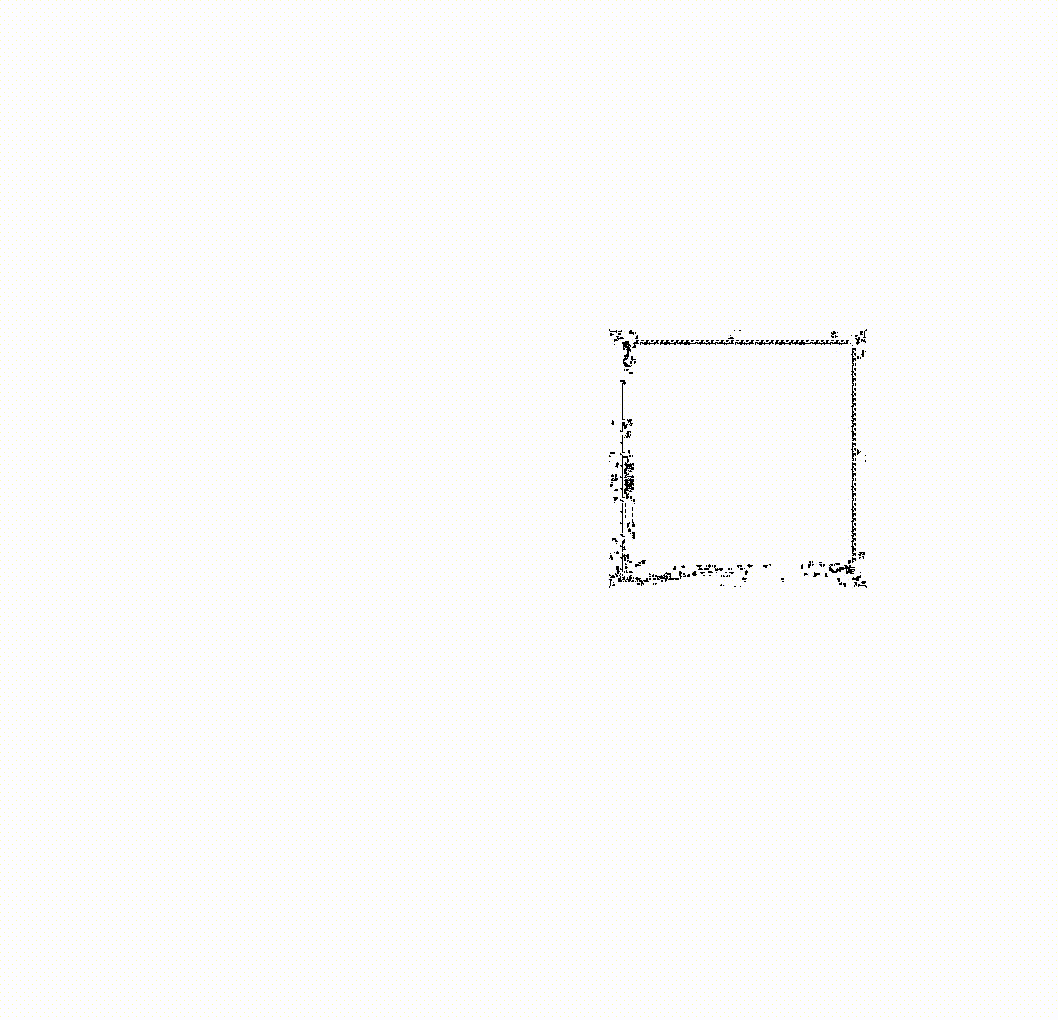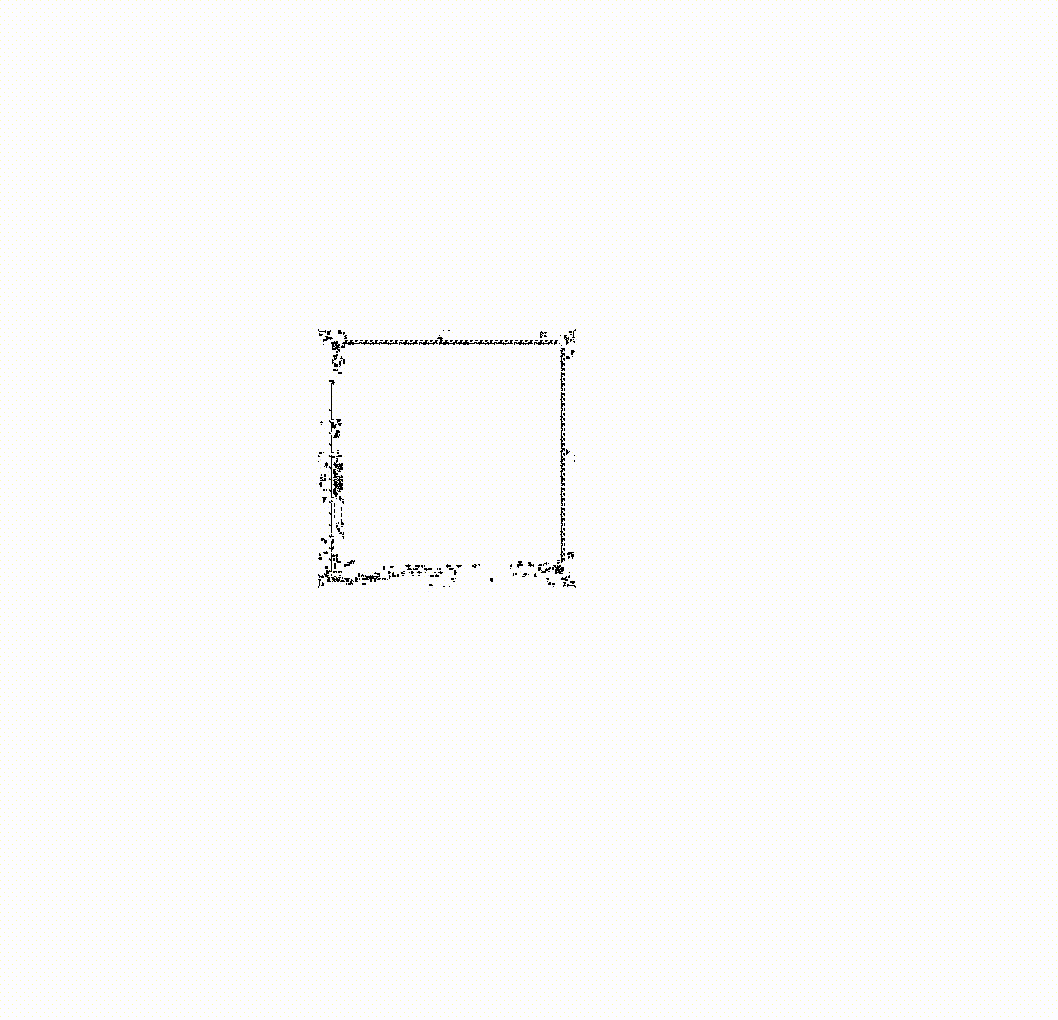
This meta-cell can be turned on and off, just like any cell it consists of. Above you see a turned-off cell; here’s what a turned-on one looks like:
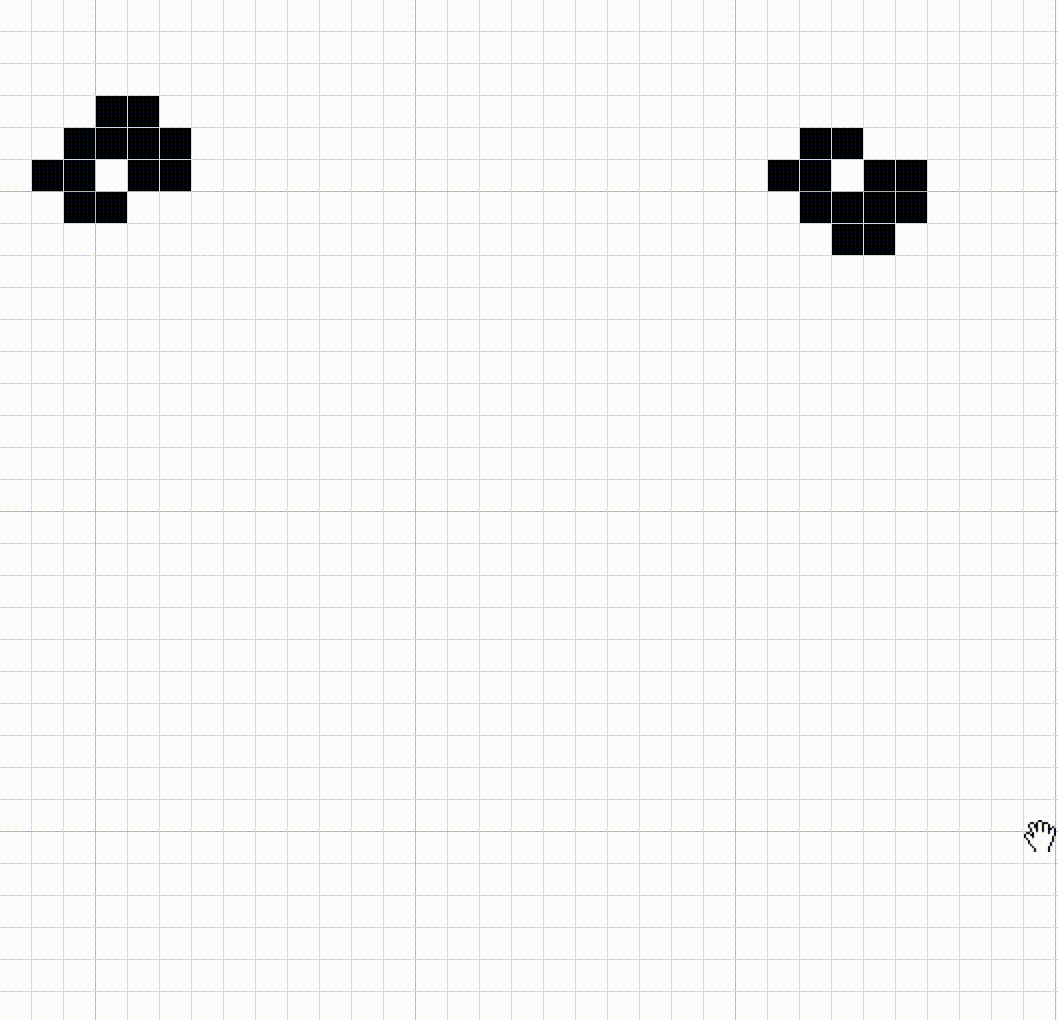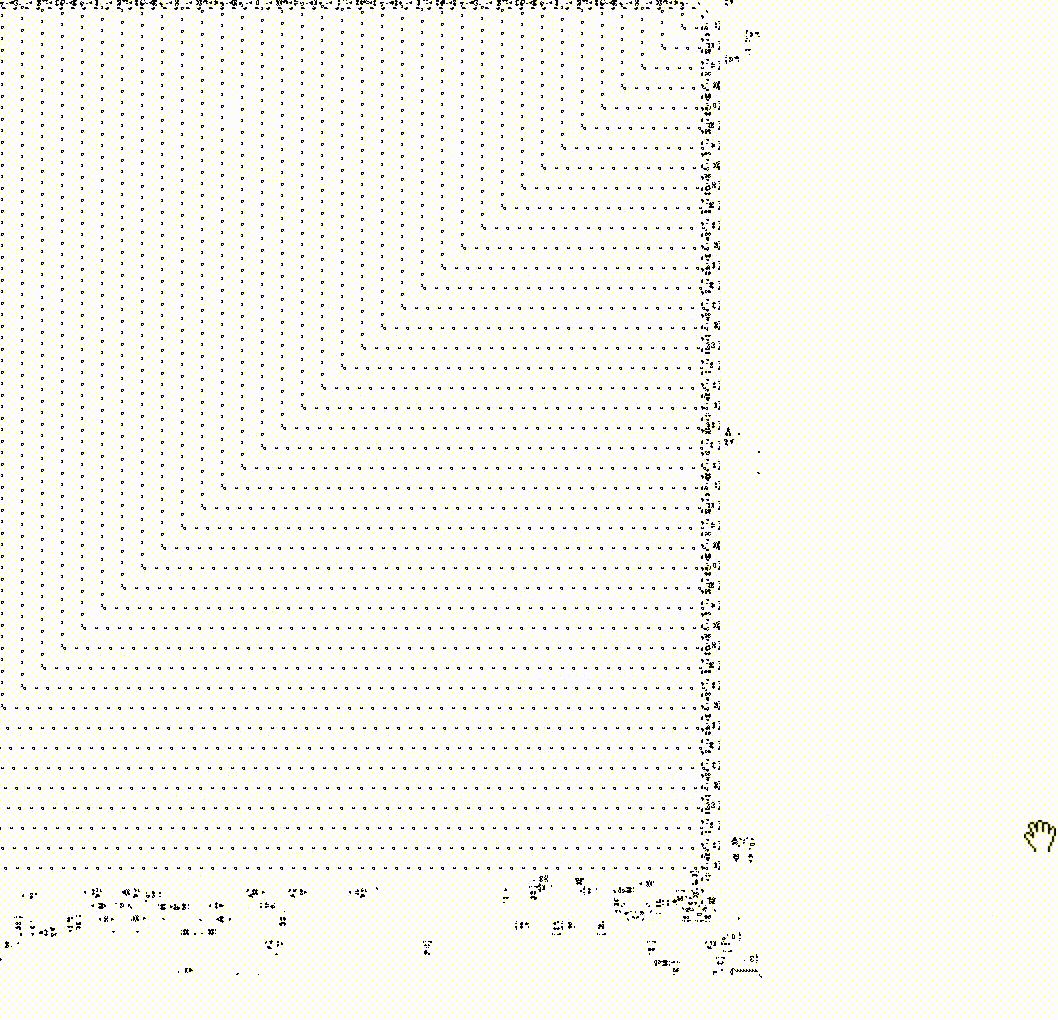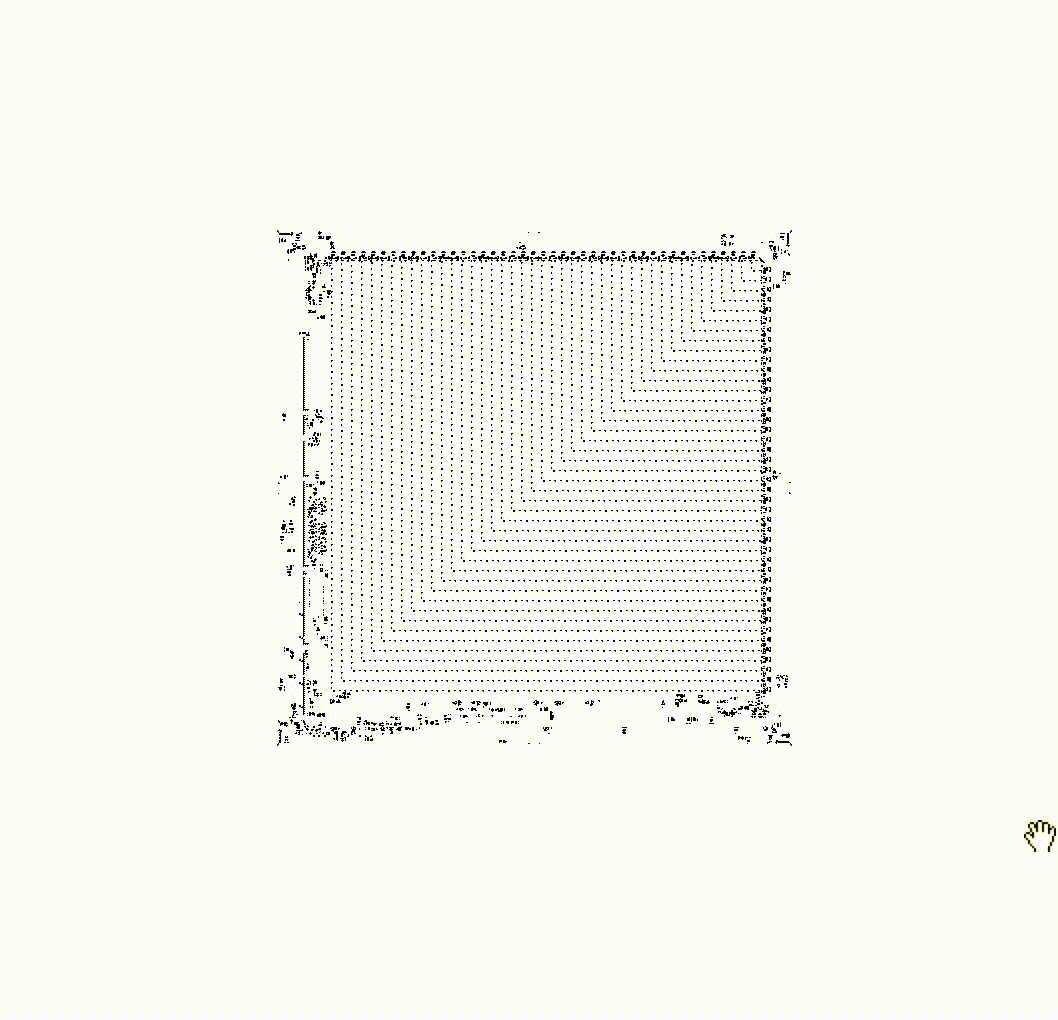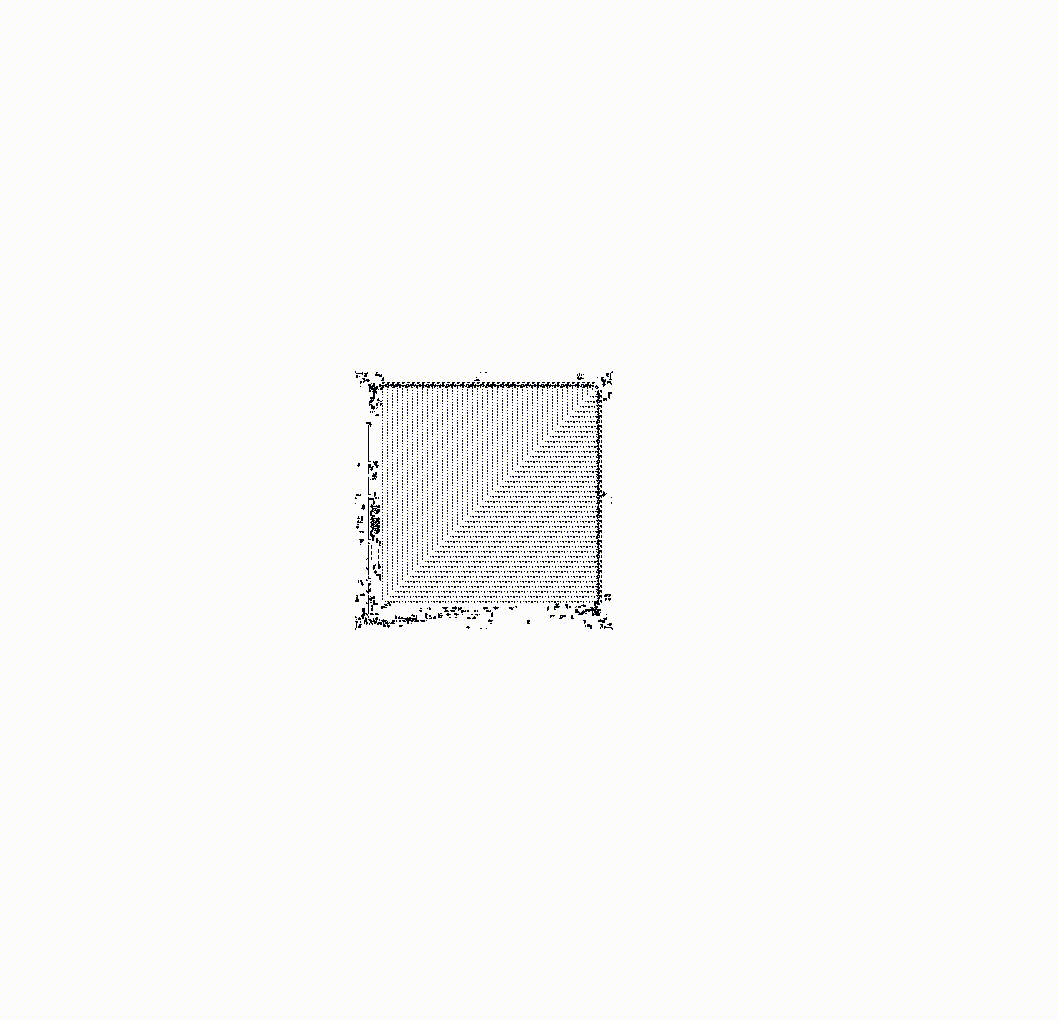
Meta-cells can communicate with each other whether they are on or off by sending gliders. Each meta-cell implements the same three rules that cells operate by on the lower level. For example, a turned-off meta-cell that receives gliders from exactly three turned-on meta-cells will turn on, thus implementing rule 3 at the meta-level. So, on a grid created by meta-cells, you can organize the same patterns as from cells at the lower level. Here, for example, is a blinker made up of meta-cells:
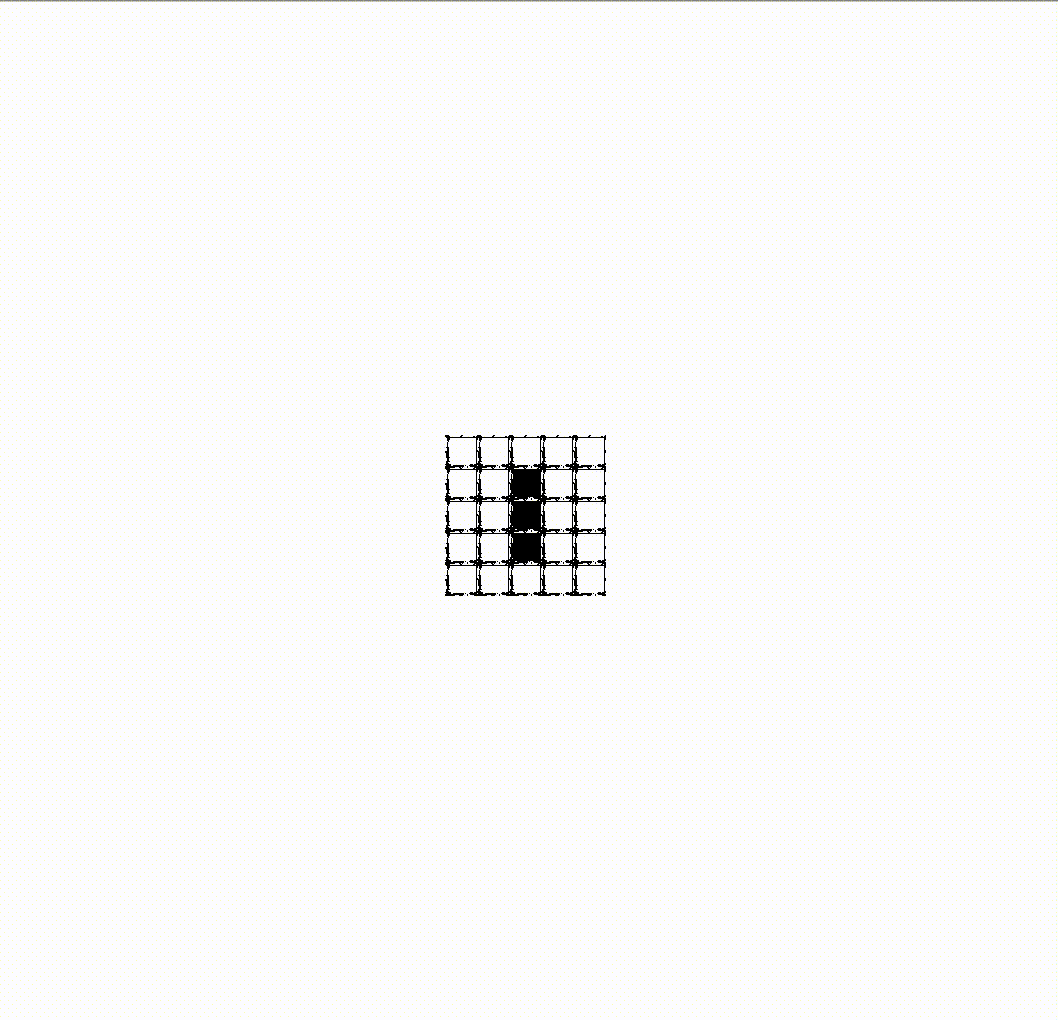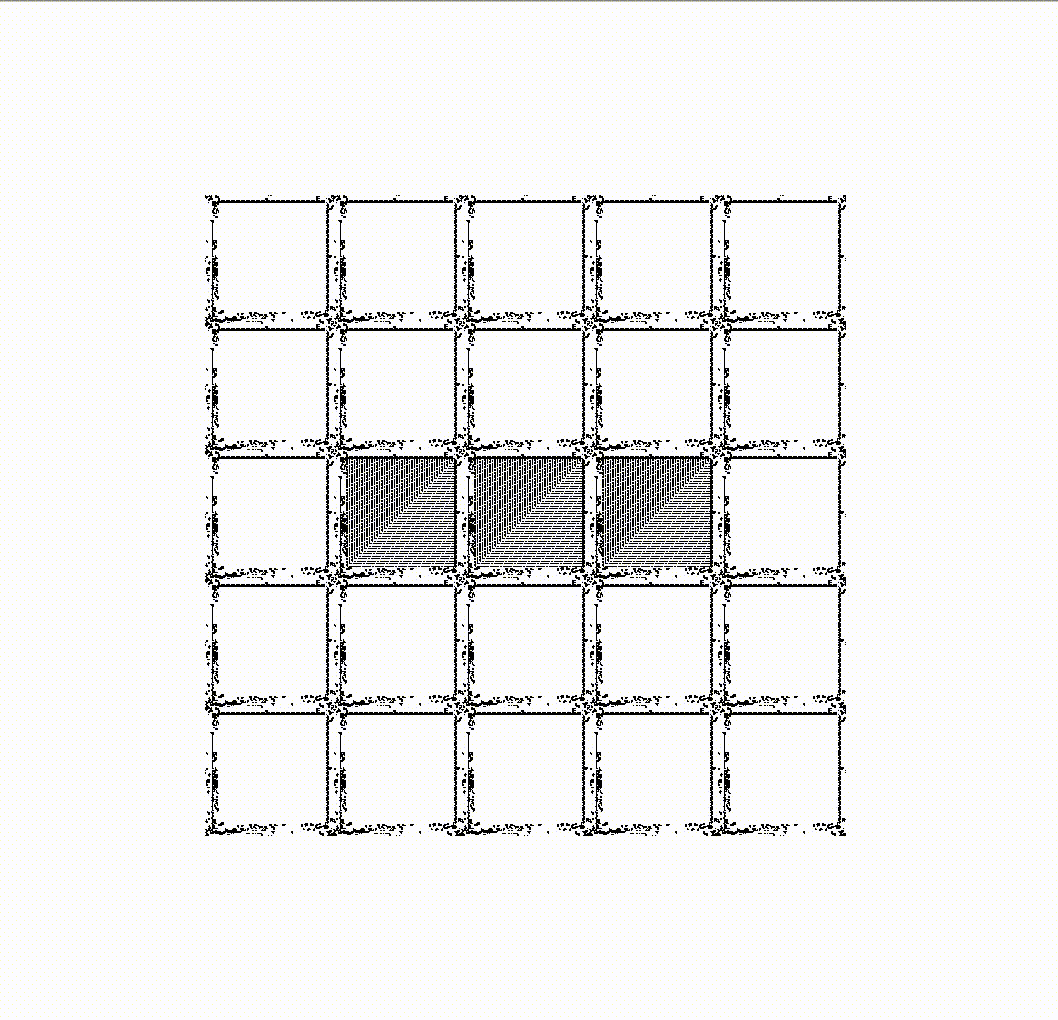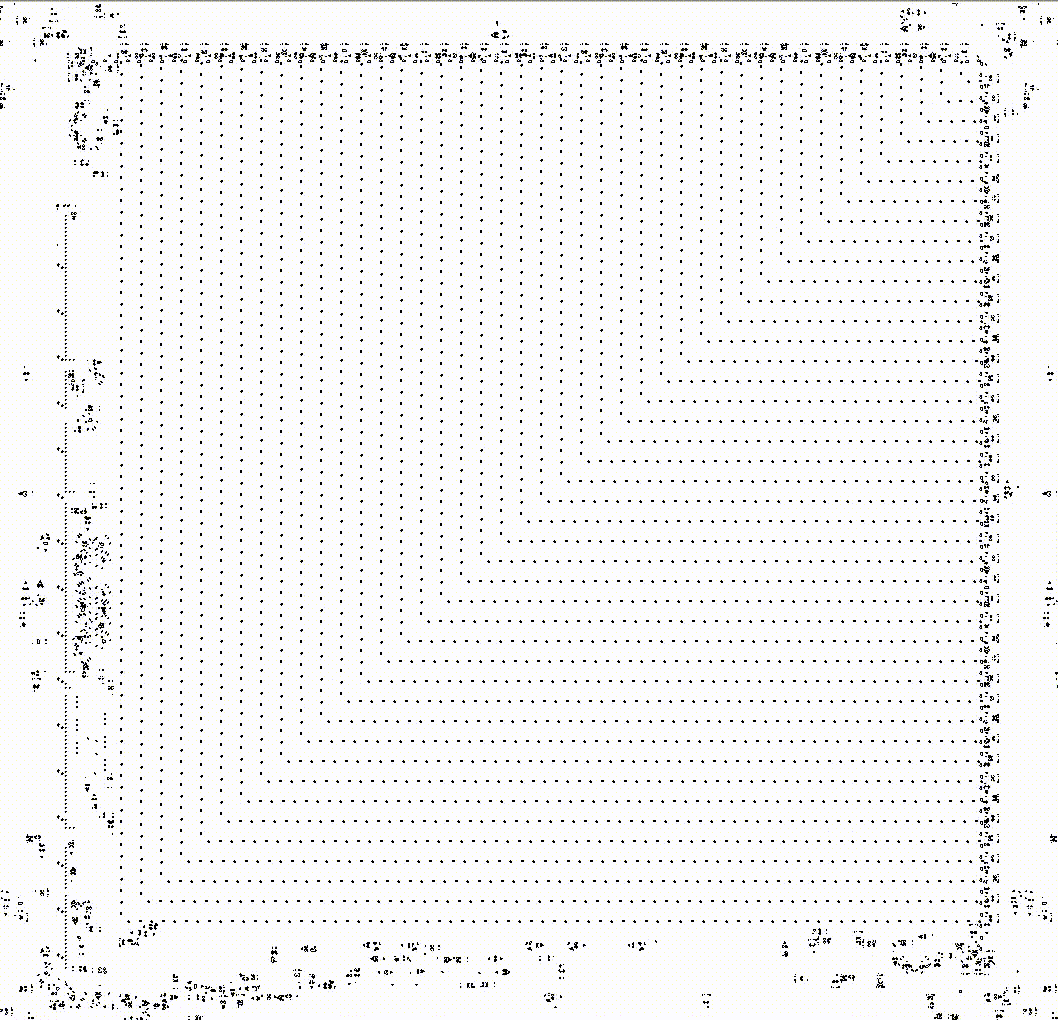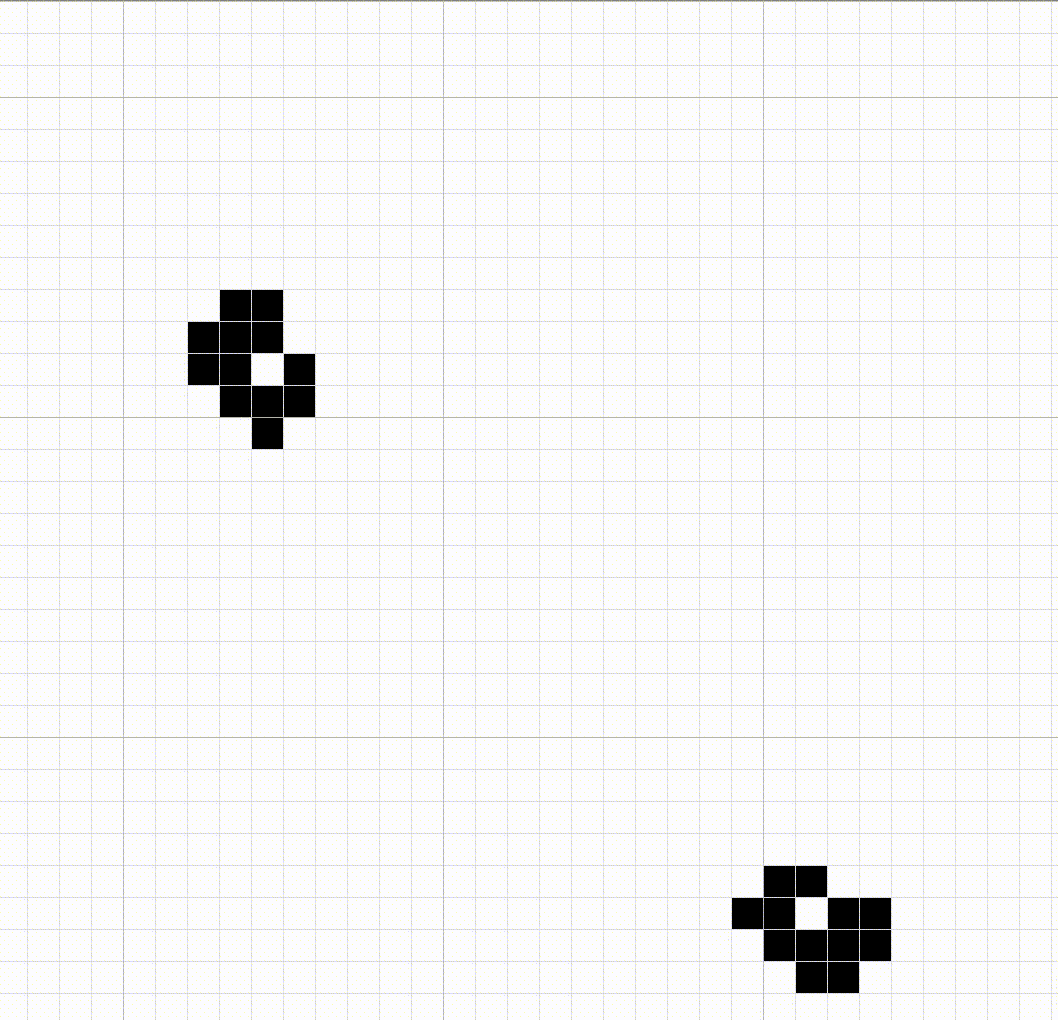
A curious reader will ask, "Can we build a meta-cell from meta-cells?" And the answer to this question is, of course, affirmative. Below is a work of engineering art demonstrating an infinite Game of Life field in which the grid is made up of meta-cells. On this grid, patterns move, which make up meta-cells at a higher level, which in turn form a grid of meta-cells, on which patterns move, which at a higher level make up other meta-cells. And so on.

Try doing zoom in and zoom out yourself in this infinite game to better understand how it works.
Analogies
We see an infinite universe that operates on three simple rules. It is very difficult for our brain to grasp infinity. Look at the night sky and try to imagine the distances to the stars, so that by the time the light from the star reaches the Earth, the star has already moved to a new place in its motion through the galaxy. The Sun was in the place we see it 8 minutes ago, and it is the closest star to us.
It seems to us that if you do zoom in for a long time, sooner or later you will reach those original cells on which the first level of the meta-cell grid is built. We are used to the idea that everything starts somewhere and ends somewhere. If you disassemble a matryoshka doll for a long time, inside will be the smallest matryoshka, which is no longer disassembled. But if the field is truly infinite, you will never reach the cells that make up everything. This is an infinite recursion that gives rise to itself. Each level is based on the previous one and creates the next one. And there is no first or last level.
We do not see infinite recursions around us. There is always a last level where recursion stops. But what if the finiteness of things is just an illusion? A convention that helps us think about the world. If you plant an acorn in the ground, and an oak tree grows from it, at what point does the acorn stop being an acorn and become a seedling, and at what point does the seedling stop being a seedling and become a tree? Can we draw clear boundaries?
In "The Heart Sutra" (Prajñāpāramitā Hridaya Sūtra), it is said, "Form is emptiness, emptiness is form. Form is not separate from emptiness, emptiness is not separate from form." And further, "There are no eyes, no ears, no nose, no tongue, no body, no mind". I’ve long tried to understand what Buddhists mean when they talk about emptiness. Does it mean that the world only seems to be there, and nothing actually exists?
It seems to us that the world consists of isolated things that exist independently. Here is a tree. It seems to exist by itself. But the tree does not exist without soil, moisture, and the sun. And it would never have appeared if not for the acorn from which it grew. And for there to be an acorn, there needs to be a tree from which this acorn fell. This means that for this to happen, life had to appear on Earth, and all these conditions from the sun, the water cycle in nature, not too hot, and not too humid climate for millions of years. Without all this, the tree simply wouldn’t exist. And strictly speaking, it didn’t appear; through the acorn, it’s a continuation of all the trees that came before it. This is an infinite transformation in which everything is connected to everything.
Mathematician Edward Lorenz, who worked on the mathematical model of global climate, introduced the concept of the "butterfly effect." A term that grew out of an academic paper he presented in 1972 entitled: "Predictability: Does the Flap of a Butterfly’s Wings in Brazil Set Off a Tornado in Texas?" Having built his model, he discovered that long-term weather forecasting is extremely sensitive to the slightest disturbances. A butterfly’s flight can change the state of the atmosphere and future weather, just as it influenced the events unfolding in Bradbury’s story "A Sound of Thunder".
In the same way, all the cells in the Game of Life are connected. Changing the state of any cell leads to a change in the state of neighboring cells, which in turn changes the state of their neighbors. So each cell is connected to every other cell in the infinite field. Move one cell and get a "П" instead of an "H," and the system behaves entirely differently. Everything depends on everything.
And since every object in the world is composed of parts, any object depends on its parts. Everything is part of something else. The higher level on our infinite Game of Life field made up of metapixels depends on the lower one, because a metacell consists of cells at a lower level. Thus, everything in the world is a temporary aggregation of parts that will eventually disintegrate to reassemble into another aggregation. Just as turning on and off cells form patterns that make up metacells, which create a grid at a higher level, cells on this grid turn on and off, forming patterns that create a grid for the next level. There is nothing that exists in isolation, and there is nothing that exists forever. Everything we see is just a temporary collection of parts, like pebbles tossed into the air for a moment to form a certain pattern.
In this way, by drawing analogies, we can look at the familiar world in a new way using the Game of Life. See that a tree, a butterfly, climate, or any object is just a pattern captured by our consciousness from the infinite transformation of an infinite number of atoms connected to each other.
From this understanding, many conclusions can be drawn. For example, I am not an isolated personality in no way connected to others. I am part of the dance of life in which everyone is connected to everyone else. All knowledge, money, and any other resources are with me thanks to other people. You read this blog because our ancestors created the language it is written in, millions of people created a huge number of technologies that allowed me to make this blog and deliver it to you. Millions of people are involved in this process alone. Next time you buy a banana in the supermarket, think about how many millions of people made it possible. We are all connected. Therefore, for example, I can be happy by making someone else happy. This simple thought can improve the lives of millions of people feeling lonely. Are you lonely? Find someone as lonely as you and smile at them, strike up a conversation. And now you are both no longer lonely.
An analogy cannot be proof of anything. The fact that the two things are similar does not yet say anything. For example, the shape of the brain resembles a walnut, and it is unlikely to mean anything. But sometimes an analogy helps to look at things in a new way. From an analogy, a hypothesis can be born. If things are similar, maybe they work the same way. The hypothesis still needs to be tested. However, having a hypothesis is already a significant step toward understanding.
In the Game of Life, we see an infinite universe that operates on three simple rules. Who knows, maybe our universe, despite its seeming diversity, is also built on very simple rules. For example, the law of conservation of energy, according to which energy does not arise and does not disappear but merely changes forms, works at both the micro and macro levels. An illustration of this can be a pendulum. When the pendulum is at the highest point of its motion, its potential energy is at its maximum, and its kinetic energy is zero. When the pendulum moves, potential energy turns into kinetic energy, which reaches its maximum at the lowest point, and then the kinetic energy begins to turn into potential energy. Similarly, an electron can move between different energy levels, which is analogous to the oscillations of a pendulum. When the electron is at a higher energy level, it has more potential energy. When transitioning to a lower level, the electron loses potential energy, which is released in the form of a photon. As stated in the Emerald Tablet "That which is above is from that which is below, and that which is below is from that which is above." This inscription is at least 1000 years old.
At some point, details matter
Mathematician Lewis Fry Richardson studied the influence of the length of national borders on the likelihood of the onset of military conflicts and noticed the following: Portugal claimed that its land border with Spain was 987 km, while Spain determined it to be 1,214 km. How can this be? The border between the countries is the same. Richardson found that this was a rounding error related to scaling. As we increase the scale, we begin to examine increasingly smaller fragments of the border, which were not visible at a coarser scale. These smaller fragments add their length to the total length of the border, leading to its increase. The larger the scale of measurement, the longer the measured border. Thus, Spanish and Portuguese geographers simply relied on measurements of different scales. What is most surprising is that as the accuracy increases, the length of the border tends to infinity.
Studying the problem of the length of the coastline of Great Britain, Mandelbrot noticed that the coastline consists of a series of bays and capes.

This is how Mandelbrot discovered fractals. A property of fractals is self-similarity, which consists of manifesting the same general figure on any scale. Regardless of how much a part of the coastline is scaled, a similar pattern of smaller bays and capes superimposed on larger bays and capes appears, down to individual grains of sand. The larger the scale, the more bays and capes, and the longer the coastline.
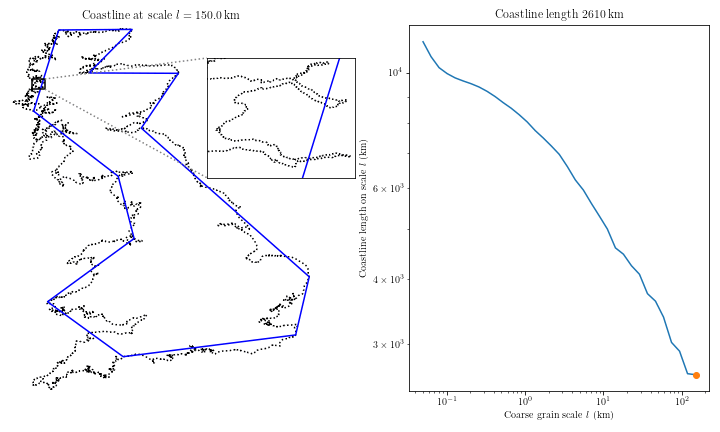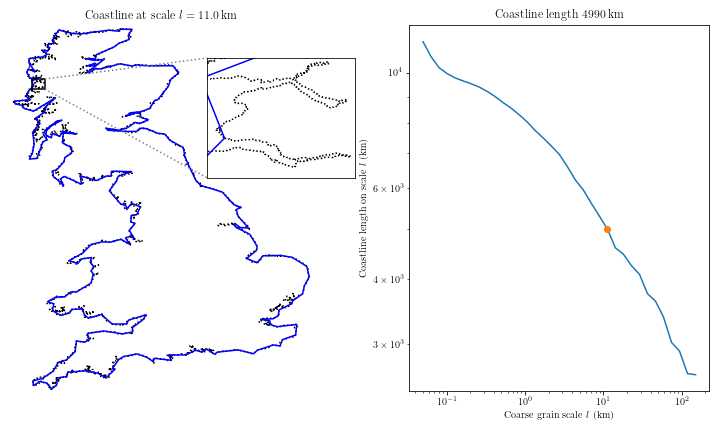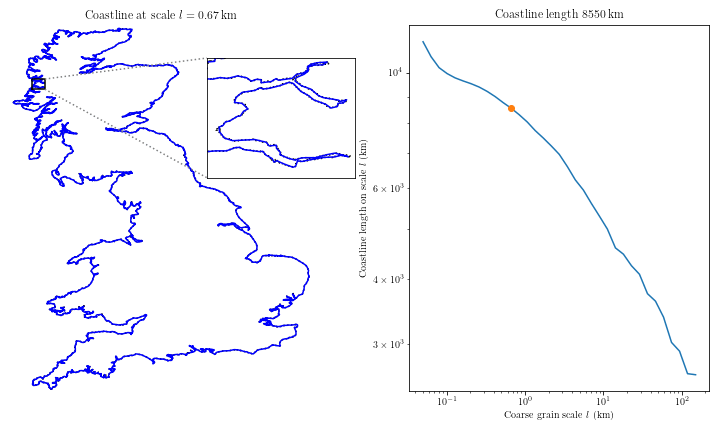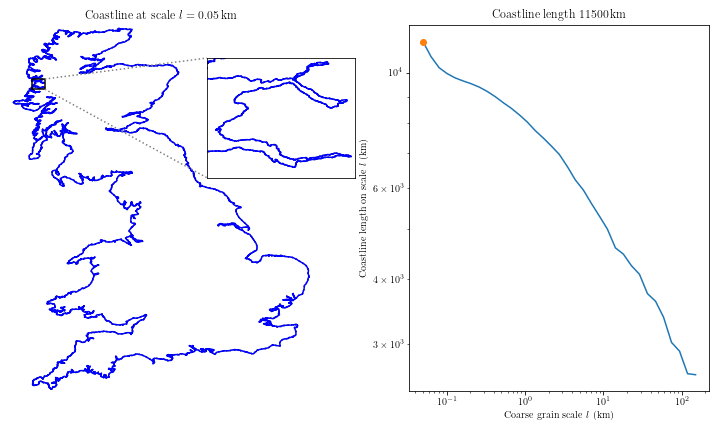
The length of the coastline or border tending to infinity is a detail that people have neglected throughout most of their history. Surprisingly, no one noticed this until the mid-20th century.
The struggle with complexity can be so engrossing that one can confuse abstraction with lossless compression. Or confuse analogy with abstraction. We may forget that our ultimate goal is not to build a coherent theory but to predict how the world works. The theory can be very elegant and well-structured, but if there are details that contradict it, they must be taken into account. In the end, we are fighting entropy, not complexity.
Abstraction in communication
Why is it important to understand at what level of abstraction you are? Building abstraction involves studying details, highlighting important ones, and discarding irrelevant ones. Very often, we assume that our interlocutor also knows all these details and understands the abstraction we are using. Abstractions greatly shorten the time required to transmit information. That’s why we create them. But often your assumption is wrong. Sometimes it takes time to go down a level and check if our understanding of the details is the same. This should be done even when the interlocutor is yourself. Sometimes it seems that we understand the details and can therefore safely use abstraction. But is this true?
Here, I must say that the demonstration of an infinite Game of Life field, where each cell recursively consists of an infinite number of meta-cells, is not the real Game of Life. It’s just a demonstration. Here, the author described how he made it, and it’s very interesting for specialists.
For non-specialists, it is worth saying that infinity is a mathematical construct. In real life, computational resources (whether computer resources or human brain resources) are limited. How we overcome this limitation in our pursuit of infinity is through technical progress and personal development for every individual.
Conclusion
Complexity is a universal phenomenon present in all areas of life, from science and technology to culture and social systems. The process of fighting entropy, the process of studying the world around us, is always a process of simplification. But you can simplify by simply avoiding complexities. Or you can dive headfirst into complexity. Marvel at the surprises of emergence, build a structure out of chaos, share your discoveries with others, get lost in layers of abstraction, stumble upon details that shatter these layers and erect new ones, draw unexpected analogies, and make new discoveries. The beauty of fractals and infinity above our heads - the world is beautiful in its complexity!
In the book "The Overflowing Brain: Information Overload and the Limits of Working Memory," Torkel Klingberg explores how the amount of information a person can temporarily store and manipulate in their mind affects cognitive abilities. It turns out that the number of objects a person can simultaneously hold in working memory directly affects their ability to think. The more objects stored in working memory, the more powerful the thinking. Every time you face complexity, it means you are up against the size of your working memory. There are so many objects that you cannot keep track of them. The good news is that working memory can be increased, thereby training your ability to think. Every time you overcome complexity, you expand the boundaries of your working memory and your thinking. Do not avoid complexity! Enjoy it!
