В окружающем мире появляется все больше возможностей, но при этом он становится все сложнее. Мы часто настолько перегружены нарастающим потоком информации, что стараемся избегать любых сложностей. В то же время для многих людей одно из самых приятных переживаний - это когда то, что было совершенно непонятным секунду назад, вдруг становится ясным. Опираясь на научные исследования, концепцию пустоты в буддизме и наблюдения за бесконечным разнообразием окружающего мира, мы с помощью неожиданных аналогий окунемся в красоту сложности. Разбирая ее роль в нашей жизни и ее влияние на наше понимание Вселенной, мы сможем лучше осознать глубокую взаимосвязанность мира вокруг нас. И я попытаюсь написать про сложность просто.
Определения
Это не научная статья, но, она так или иначе касается науки, поэтому как настоящие ученые, давайте начнем с определений. Если мы проскочим этот шаг, то может оказаться что мы понимаем по-разному ключевые понятия, а они фундамент, на котором все держится. В то же время, я не могу быть совсем точным в определениях, чтобы не скатиться в формулы и математику. Я постараюсь балансировать между тем, что известно всем и точностью формулировок.
Энтропия
Чем занимаются ученые? На самом деле тем же, чем и любые другие живые существа. Ученые пытаются понять законы, по которым работает мир, чтобы научиться предсказывать будущее. Зачем нужно предсказывать будущее? Чтобы минимизировать потери из-за неожиданных сюрпризов и максимизировать доступные ресурсы. Никто не любит терять и нуждаться. А мир хаотичен и непредсказуем.
Противоположностью предсказуемости является энтропия. На эволюцию живых существ можно посмотреть существ как на борьбу с энтропией. Например, у древних членистоногих называемых трилобиты, в ходе эволюции развился глаз, состоящий из множества гранёных линз, что позволило им лучше ориентироваться в морском пространстве, активно искать пищу и избегать хищников. Это привело к увеличению выживаемости трилобитов и их доминированию в морских экосистемах в течение долгого времени. Так особи без глаз не выжили, а особи с глазами размножились и передали свою находку потомкам, которые таким же образом эту находку улучшали. Случайные мутации приведшие к появлению глаза закрепились, а особи без такой мутации отсеялись.
Эволюция процесс долгий. Человек борется с энтропией посредством создания и накопления знания. Это гораздо более быстрый процесс, поскольку не нужно ждать долгой смены поколений, но в целом он похож на эволюцию живых существ. Люди выдвигают теории о том как работает мир, а потом проверяют на сколько они действительно предсказывают будущее. Те, что предсказывают плохо - отсеиваются или видоизменяются, чтобы делать лучшие предсказания. Так теории эволюционируют, а энтропия снижается.
Информация и сложность
Вы вынимаете носки из стиральной машины. Что быстрее - отсортировать их и сложить парами в ящик или засунуть не сортированную кучу и каждый раз искать носочку пару? С точки зрения экономии времени по утрам - первый вариант предпочтительнее. Но с точки зрения сложности - разницы нет. Вы можете отсортировать сразу и потратить на это много времени или выполнять шаг сортировки раз в день и каждый день тратить по чуть-чуть. Количество операций при этом одинаковое и сложность одинаковая.
Мы видим, что, чтобы преодолеть энтропию, которую создала нам стиральная машина, нужно выполнить некоторые действия.
Что делают ученые для преодоления энтропии некоторого явления, которое они не понимают и поэтом не могут предсказывать? Совершают действия в виде получения информации.
Как правило, ученые изучают взаимодействие некоторых сущностей между собой. Совокупность взаимодействующих сущностей называют системой. В нашем случе - это носки, которые ищут себе пару. Поскольку почти все, что нам может встретиться во Вселенной можно разделить на части, вся вселенная - это системы и взаимодействия.
Информация - это то, что позволяет уменьшить неопределенность в системе. Можно сказать, что информация - это уменьшение энтропии системы. Чем больше информации, тем меньше энтропия.
Сложность - это мера того, насколько трудно понять или определить систему. Чем сложнее система, тем больше информации необходимо для ее описания или понимания. Если у вас все носки одинаковые, то на сортировку вы потратите очень мало времени. Любые два носка составляют пару. Если у вас как у меня носки разноцветные, то отсортировать их значительно сложнее. Зато я могу сообщить миру гораздо больше информации надевая веселенькие или грустненькие носочки в зависимости от настроения.
Таким образом, энтропия, информация и сложность связаны между собой. Энтропия и сложность взаимосвязаны, поскольку сложные системы, как правило, имеют более высокую энтропию. Информация уменьшает энтропию и упрощает сложность, делая систему более понятной и организованной.
Способы борьбы со сложностью
Хорошо, с терминами определились. Переходим к самому интересному. На пути преодоления энтропии, приходится преодолевать сложность. Эволюция живого и эволюция человеческого знания нашли много способов бороться с ней.
Разделяй и властвуй структурируй
Когда вы впервые начинаете изучать иностранный язык, все может показаться сложным и непонятным. Вы слышите речь носителя языка и для вас это просто поток звуков.
Однако, если вы будете изучать язык по частям, делая шаг за шагом, то вскоре начнете замечать прогресс. Вы начинаете с основ, таких как алфавит и фонетика, затем постепенно переходите к изучению грамматики, расширению словарного запаса и улучшению навыков общения. В результате разбивая этот сложный процесс на мелкие и понятные части, вы начинаете понимать иностранный язык и в конечном итоге можете свободно общаться на нем. Теперь из потока звуков вы легко вычленяете слова и предложения. Вы не можете поверить, что когда-то не понимали этот язык!
Шаги изучения связаны между собой. Без знания алфавита вряд ли стоит браться за грамматику. Каждый из шагов разбивается на более мелкие.
Обобщая, можно сказать, что мы стремимся структурировать информацию. Например, этот пост обладает некоторой структурой. В нем есть заголовки и подзаголовки. Мы начали с простых терминов и сейчас углубляемся в примеры.
В общем этот метод познания очень хорошо описал Рене Декарт в 1637 году: "делить каждую из рассматриваемых мною трудностей на столько частей, сколько потребуется, чтобы лучше их разрешить" и "располагать свои мысли в определенном порядке, начиная с предметов простейших и легко познаваемых, и восходить мало-помалу, как по ступеням, до познания наиболее сложных, допуская существование порядка даже среди тех, которые в естественном ходе вещей не предшествуют друг другу."
И этот метод работал настолько хорошо, что в какой-то момент ученым показалось, что они уже практически все изучили. Вот несколько цитат
Альберт Абрахам Майкельсон: "Кажется вероятным, что большинство главных базовых принципов были твердо установлены и что дальнейшие успехи должны быть найдены в основном в строгом применении этих принципов ко всем явлениям, которые попадают под наше внимание. Именно здесь наука об измерении демонстрирует свою важность - где количественная работа предпочтительнее качественной работы. Выдающийся физик заметил, что будущие истины физической науки следует искать в шестом знаке после десятичной точки." (1894, dedication of Ryerson Physical Laboratory, quoted in Annual Register 1896)
Хендрик Антон Лоренц: "Согласно нашим нынешним взглядам, все основные законы природы были обнаружены и проверены. Существующие эксперименты не свидетельствуют о том, что будут обнаружены какие-либо новые принципы. Следовательно, мы можем сказать, что законы природы в их окончательной форме известны, и что открытие новых взаимосвязей внутри них, а также отклонения от них, которые еще необходимо точно определить, являются единственными задачами, которые все еще ждут физика. Исследование этих задач неизбежно приведет к более глубокому пониманию основ физики." (Лоренц, Г.А. "Настоящий статус проблем излучения." Нобелевская лекция, 1902)
Буквально вскоре Эйншейн опубликовал свою теорию относительности и появилась квантовая механика. Мир, который казался таким понятным и предсказуемым, открыл ученым сколько еще в нем скрытой энтропии. До сих пор они пытаются вывести стройную и не противоречивую теорию объединяющую все эти открытия.
Кажется, мы не можем просто разбивать что-то сложное на маленькие части и быть уверенными, что из них потом получится цельная картина.
Эмерджентность
Представьте себя ученым, изучающим красных огненных муравьев. Вы разбираете их поведение, анатомию и общественную структуру. У муравьев есть определенные свойства, например, они живут в колониях, имеют разделение труда между рабочими, солдатами и королевой. Их программа действий кажется простой: искать пищу, заботиться о потомстве и защищать гнездо. Изучив их отдельные характеристики, вы можете подумать, что уже все знаете про них и предсказать их поведение в различных ситуациях. Ваши предсказания даже хорошо работают.
Но вот приходит наводнение, и вы думаете, что они все погибнут, так как их простая программа действий не предусматривает адаптацию к таким условиям. Однако, вместо того чтобы погибнуть, они объединяются и образуют новую структуру, которая никак не следует из их простых свойств. Эта структура называется "живой плот". Вот как она выглядит:

Живой плот – это конструкция из муравьев, которые связывают себя друг с другом, используя свои лапы и тела, образуя плавучую платформу, способную удерживать всю колонию над водой. Это явление - пример эмерджентности, когда новые свойства и качества возникают из взаимодействия простых компонентов. В данном случае, простые свойства и поведение отдельных муравьев не предсказывали бы возникновение такой сложной адаптивной структуры, как живой плот.
Эмерджентность - это тот самый сюрприз, который можно получить после того как изучил каждый отдельный компонент системы и подумал, что теперь понимаешь всю систему целиком. Если вы оглянетесь вокруг, то скорее всего увидите плоды трудов миллионов людей. Дома, машины, интернет, спутники и самолеты, летающие над вашей головой. Сложно поверить, что прямоходящая обезьяна, которая очень медленно бегает, имеет маленькие клыки и слабые мышцы смогла построить все это. Это все пример объединения и совместной работы. Пример борьбы эмерджентности с энтропией.
Сжатие без потерь
Каждый раз, когда я вижу в магазине Romanesco broccoli я долго не могу от него оторвать взгляд.
.jpg)
Хочется любоваться этой красотой бесконечно. Фигура эта очень сложная, это вам не простой шар (такой, как арбуз) или параллелепипед (как пакет молока). Но много ли информации надо, чтобы объяснить как она устроена? Насколько она сложнее чем арбуз?
Сегодня на прогулке я сфотографировал дерево. Взгляните на любую ветку, которая отходит от ствола. Она выглядит как дерево в миниатюре.

Еще Леонардо Да Винчи в своих записках писал:
Сумма толщин всех ветвей дерева на каждом этапе его высоты равна толщине ствола [ниже них].
А теперь давайте сравним фото дерева с фото Лонг-Айленда (Багамские острова).

В этой же самой записи Леонардо продолжил
Объем всех ответвлений водного [потока] на каждом этапе его движения, равен объему основного русла.
Удивительно, что эти идеи не получили особого развития до середины 20-ого века, а объекты такие даже не имели никакого названия. Их заметил и начал изучать математик Бенуа Мандельброт. Он назвал свою находку фракталами. Фрактал — это геометрический объект, который обладает свойством самоподобия, то есть его части повторяют форму целого объекта на разных уровнях масштаба. Фракталы часто используются для описания сложных форм, которые не могут быть представлены простыми геометрическими фигурами, таких как линии, круги или прямоугольники. Увидев фракталы один раз, вы будете видеть их везде. Ветви деревьев и молнии, снежинки и иней на окне, дельты рек и легкие человека, горные хребты и облака.
Я написал маленькую программу, которая строит дерево. Давайте запустим ее, чтобы понять как появляются фракталы.
Нажмите на кнопку "Старт" внизу, чтобы увидеть этот алгоритм в действии.
Это не анимация, это реальный код на языке Javascript. В нем реализована функция, которая рисует ветвь с заданным углом и длиной от начальной точки с некоторыми начальными координатами (startX, startY). Затем она вызывает сама себя дважды для каждой из двух новых веток, уменьшая длину веток на 30% и изменяя угол ветвления на 30 градусов. В качестве начальной точки для новых веток (startX, startY), передается конечная точка текущей ветки (которая определяется ее начальными координатами, длиной ветки и углом наклона). Процесс повторяется для каждой из веток. Этот процесс, когда функция вызывает саму себя, называется рекурсией.
Так, имея всего одну функцию, мы можем описать все дерево. Нам не нужно заранее просчитывать координаты и наклон всех ветвей, каждая ветвь рисует себя. Она не знает, да ей и не нужно знать ничего о всем дереве. Ветвь имеет функцию, которая ее нарисовала и вызывает эту функцию для того, чтобы нарисовать еще две ветки похожие на нее, но меньших размеров и с другим углом наклона. Поскольку новые ветви - это уменьшенная копия текущей, то вся информация (начальные координаты, наклон, длина ветви) на каждом шаге есть.
Для того чтобы понять как устроена фрактальная структура, нам нужно понять как работает этот один шаг. И все. То, что выглядит очень сложным, становится очень простым.
Одну и ту же систему можно описать по-разному, создав при этом разное количество информации, а значит, как правило, разную сложность. Дерево можно описать во всех деталях, а можно описать как выглядит первый шаг и рекурсия. Вы сжимаете информацию без потери ее способности описывать систему, что делает систему более понятной. Первый вывод - сложность это не только про саму систему, сложность зависит от того, кто постигает систему, потому что важно как он или она это делает.
Как я уже говорил, поняв один раз что такое фрактал, вы будете видеть его везде. Если вы оглянетесь вокруг, то увидите древовидные структуры на каждом шагу. В организациях есть начальник, его замы, замы замов и так далее. Эволюцию чего угодно можно представить как дерево, в котором каждая ветка - это путь от одной мутации до другой. Система рек, кровеносных сосудов, электрических сетей тоже имеет древовидную и очень похожую структуру. Почему она так распространена?
Рекурсивные структуры имеют преимущества, такие как эффективное использование ресурсов. Они обеспечивают оптимальное использование пространства и материалов, предоставляя максимальную поверхность при минимальном количестве материала.
Такие структуры также обеспечивают адаптивность и гибкость. Они позволяют системам приспосабливаться к изменяющимся условиям. Например, разветвление реки находит путь наименьшего сопротивления, а разветвление дерева оптимизирует поглощение солнечного света для фотосинтеза.
Как мы уже отмечали, еще один пример использования древовидной структуры - это пост, который вы читаете. Здесь есть заголовки и подзаголовки. Древовидная структура часто используется для организации знаний. Почему мы так делаем? Это может стать интересной пищей для размышлений.
Абстракция
"Но деревья не выглядят в реальности такими ровными, каким построил дерево наш рекурсивный алгоритм", — возразите вы и будете правы. Да, мы пренебрегли некоторыми деталями. Ученые очень часто так делают. Вместо того чтобы изучать реальность во всех ее деталях, они строят некоторую модель, которая в некоторой степени отражает некоторые свойства реальности. Звучит не очень надежно. Что если мы пренебрежем существенными деталями? Так может случиться, но мы не знаем заранее что существенно, а что нет. А деталей настолько много, что какими-то из них придется пренебречь. Поэтому мы строим какую-то модель, и смотрим на сколько она отражает действительность. Если действительность нас удивляет, значит наша модель не учитывает тех самых важных деталей.
Что дает нам такая абстракция как фрактал? Пренебрегая деталями, мы увидели, что деревья, кустарники, реки, кровеносная система, организации - все имеют одинаковую структуру. А значит велика вероятность, что хорошо поняв эту структуру, мы поймем сразу много областей реальности, которые работают одинаково.
Абстракция - это процесс упрощения или обобщения сложных объектов, ситуаций или концепций, позволяющий сосредоточиться на основных характеристиках и отсеять незначительные детали. Вам не нужно знать внутреннее устройство автомобиля, чтобы на нем ехать. Даже такими деталями как едет ли он на бензине или электричестве, можно пренебречь до тех пор, пока не пришло время автомобиль заправлять. Мы применяем абстрагирование везде.
По сути язык - это тоже абстракция. Каждому объекту реальности соответствует одно или несколько слов в языке. Но слова формируют разные образы у разных людей. Если я скажу «стол» вы представите себе не тот же стол, что я. Мы сжимаем реальность, а потом разжимаем ее с некоторыми потерями. Так мы выражаем одни абстракции с помощью других, стараясь найти баланс между упрощением и точностью.
Игра жизнь
Чтобы лучше понимать сложность и то, как ее можно моделировать, давайте посмотрим на одну очень известную модель, которая называется "Игра жизнь". Ее придумал английский математик Джон Конвей в 1970 году.
На двумерном поле, представляющем собой сетку, каждая клетка может находиться в одном из двух состояний: быть "живой" или "мертвой". Переход от одного состояния к другому происходит в зависимости от состояния соседних клеток.
Правила "Игры Жизнь" просты и основываются на следующих принципах:
-
Выживание. Каждая клетка, имеющая вокруг себя две или три соседние живые клетки, выживает.
-
Гибель. Каждая клетка, у которой больше трёх живых соседей, погибает из-за перенаселённости. Каждая клетка, вокруг которой свободны все соседние клетки или же занята всего одна клетка, погибает от одиночества.
-
Рождение. Если число живых клеток, с которыми граничит какая-нибудь пустая клетка, в точности равно трём (не больше и не меньше), то на этой клетке происходит рождение нового «организма», то есть следующим ходом она оживает.
Важно понять, что рождение и гибель всех «организмов» происходит одновременно. Вместе взятые, они образуют одно поколение или один ход в эволюции начальной конфигурации.
Игра Жизнь не имеет конкретной цели и не является игрой в обычном понимании этого слова. Она скорее является математической моделью, которая используется для изучения динамики систем и самоорганизующихся процессов. В зависимости от начальной конфигурации клеток, "Игра Жизнь" может привести к различным результатам: стабильным структурам, колебательным фигурам или хаотическим образованиям.
Попробуйте угадать что будет происходить на поле, а потом нажмите кнопку Старт и проверьте свою догадку.
Средняя клетка всегда имеет двух соседей и выживает согласно правилу 1. Живые клетки, имеющие общие стороны со средней клеткой, умирают из-за одиночества (правило 2), а мертвые клетки возрождаются благодаря трём соседям (правило 3), что вызывает переключение между горизонтальным и вертикальным состояниями фигуры. Мы получаем мигающую фигуру. Конвей назвал ее мигалка (Blinker).
Добавим одну клеточку и получим совершенно другую картину.
Колебания пропали. Популяция устойчива.
В следующем примере популяция клеток за несколько шагов полностью исчезает.
Но поменяем всего одну клетку, из "Н" сделав "П", и ситуация меняется совершенно непредсказуемым образом.
Всего одна клетка на новом месте и вместо смерти, очень бурная жизнь, которая через много итераций приводит популяцию в устойчивое состояние. Если это удивило вас, то вы испытали те ощущения, которые испытывают исследователи, натыкающиеся на эмерджентные состояния.
Очень простые правила приводят к очень сложному поведению, которое невозможно предсказать, потому что зачастую число вовлеченных клеток растет так быстро, что выходит за пределы человеческих возможностей, а иногда и за пределы существующих компьютерных мощностей.
Оказалось, что Игра Жизнь отлично подходит для моделирования процессов, происходящих в реальности. Распространение пожаров, слухов, эпидемий, раковых клеток, коррозии в металлах, транспортные пробки на дорогах, самоорганизация паттернов в природе (например, узоры на раковинах моллюсков и крыльях бабочек) и в обществах, моделирование изменения климата и температурных аномалий, развитие городской инфраструктуры.
Находились все новые и новые интересные паттерны. Вот, например "планер" (glider)

паттерн, который через несколько шагов воспроизводит сам себя, но в новом месте и таким образом движется по полю.
Во всех экспериментах, что видел Джон Конвей, популяции клеток либо полностью исчезают, либо стабилизируются и дальше не меняется. Так же есть правило 2 согласно которому клетки умирают из-за перенаселенности. Исходя из этого, он предположил, что количество живых клеток всегда ограничено. Конвей считал, что число живых клеток не может расти бесконечно. Он даже предложил премию тому, кто опровергнет его гипотезу. Вскоре он выплатил премию. Группа из MIT придумала ружье, стреляющее планерами (Gospers glider gun).
Поскольку количество планеров, вылетающих из ружья, бесконечно, то и число живых клеток будет бесконечно расти.
Очень удобно, когда строить теории и опровергать их можно таким наглядным образом.
И вы могли заметить, что мы все меньше думаем в терминах клеток и все больше - в терминах паттернов, в которые клетки выстраиваются. С уровня взаимодействия клеток мы поднялись на новый уровень абстракции - взаимодействия паттернов.
Не могу удержаться и не пойти в эту тему чуть глубже. Людям далеким от программирования или математики, она может показаться сложноватой или слишком абстрактной. В таком случае смело проматывайте до следующего пункта Бесконечные игры
Переходя с уровня клеток, на уровень паттернов, мы замечаем, что ружье Госпера стреляя планерами, может передавать информацию из одной части поля в другую. Сталкиваясь, планеры нейтрализуют друг друга, так сигнал можно "выключить".
Клетка - это статическое состояние включен-выключен. Ружье Госпера позволяет нам эти включен-выключен передавать на расстоянии.
Если присмотреться к Игре Жизнь, то можно увидеть ее сходство с компьютером. В компьютере вся информация хранится в виде битов, которые могут быть 0 или 1 точно так же как клеточка может быть закрашена или нет. Группу битов можно интерпретировать совершенно разными способами. Например, если позиция каждого бита - это степень числа 2, то группу из трех битов 101 можно интерпретировать как число 5 (поскольку 1×22 + 0×21 + 1×20 ) и так можно представить любое число (более того, так числа в вашем компьютере и представляются). С помощью ружей Госпера можно сделать логические операции в Игре Жизнь. Из логических операций можно строить цепочки и создавать таким образом любые программы. Например, калькулятор, который совершает вычисления над числами, закодированными в клетках. Так, игра, построенная на трех простых правилах, превращается в вычислительную машину, на которой можно запрограммировать все что угодно. Это еще один пример эмерджентности.
Бесконечные игры
В 2006 году был опубликован паттерн OTCA metapixel. Он занимает 2048х2048 клеток и является метаклеткой. Т.е. это клетка состоящая из клеток.
Эта метаклетка может быть включена и выключена, точно так же как любая клетка, из которых она состоит. Сверху вы видите выключенную клетку, вот так выглядит включенная:
Метаклетки могут сообщать друг другу включены они или выключены, посылая глайдеры. Каждая метаклетка реализует те самые три правила, по которым работают клетки на нижнем уровне. Например, выключенная метаклетка, в которую пришли глайдеры от ровно трех включенных метаклеток, включается, реализуя таким образом правило 3 на метауровне. Так что на сетке, построенной из метаклеток, можно организовывать те же паттерны, что и из клеток на нижнем уровне. Вот, например, мигалка, составленная из метаклеток:
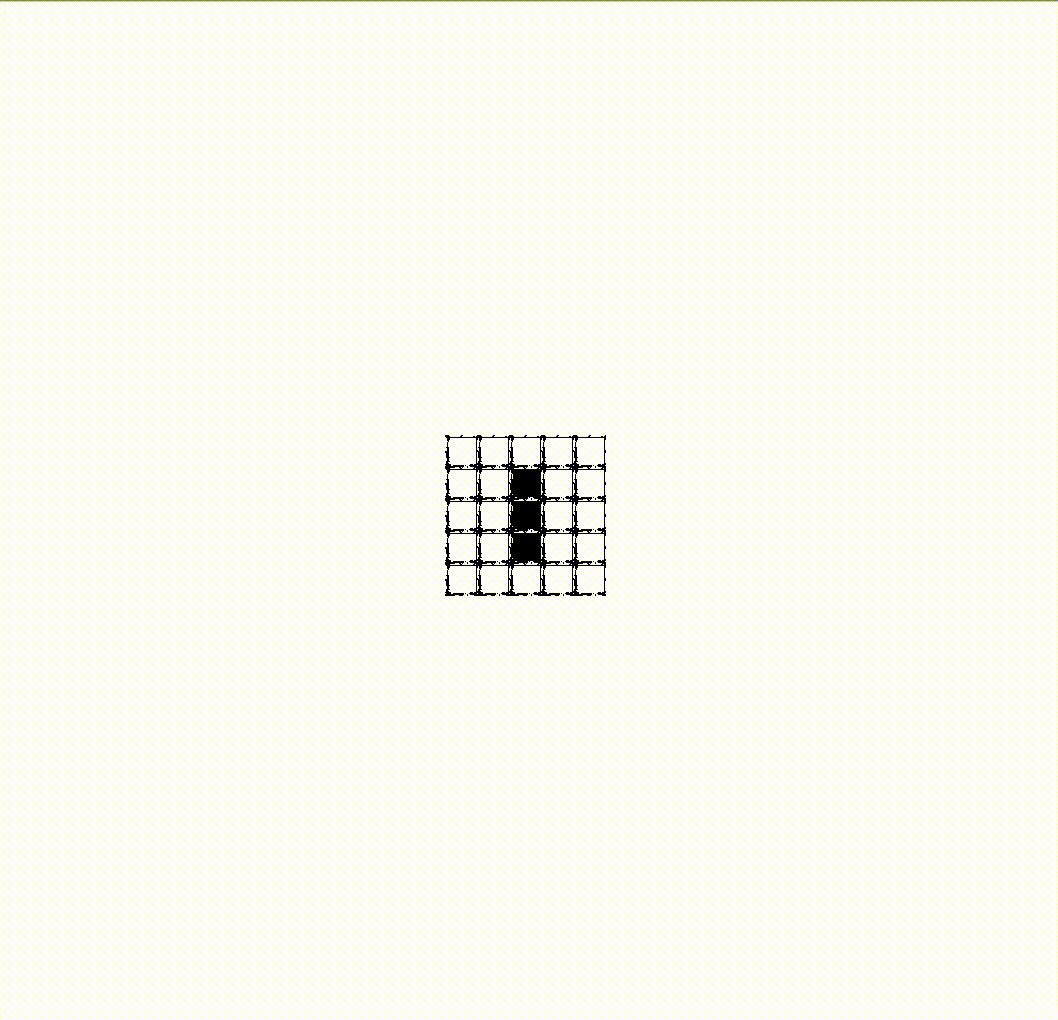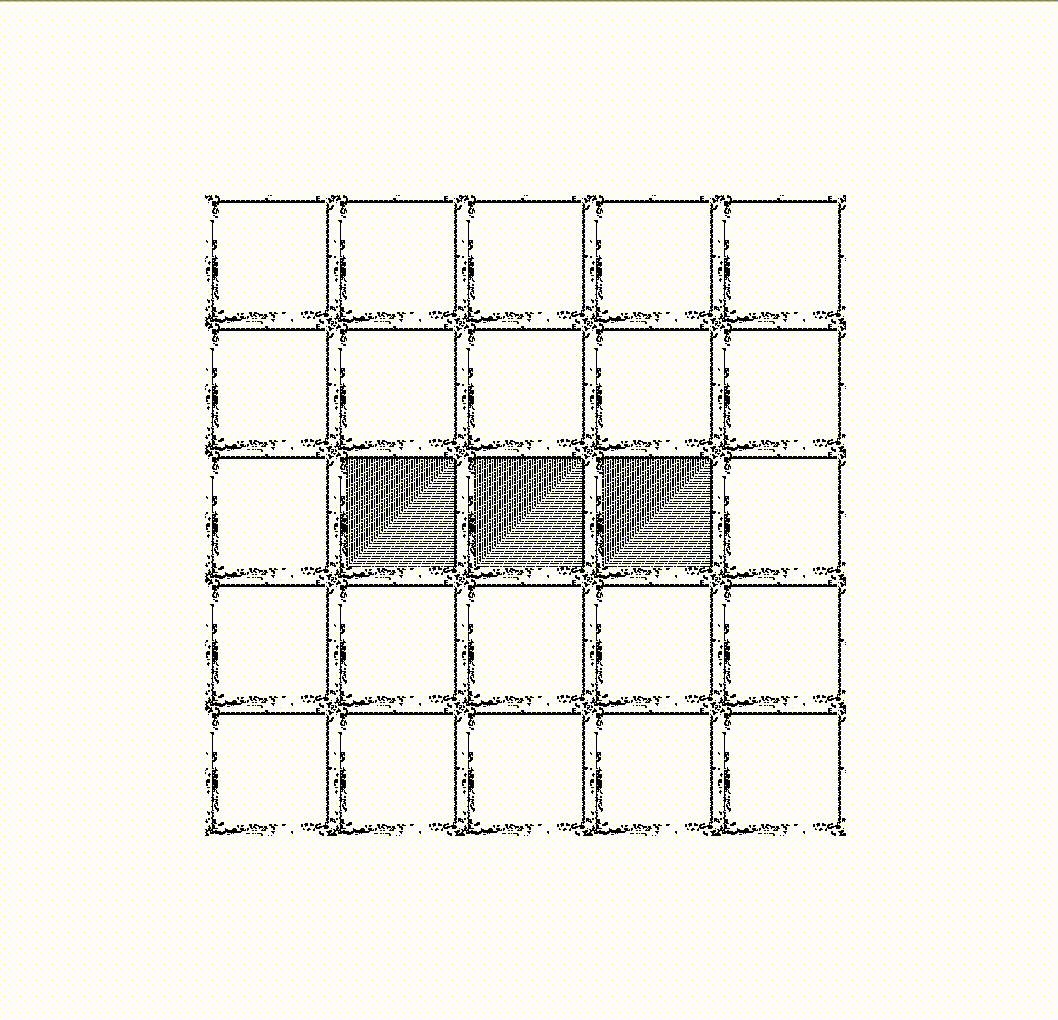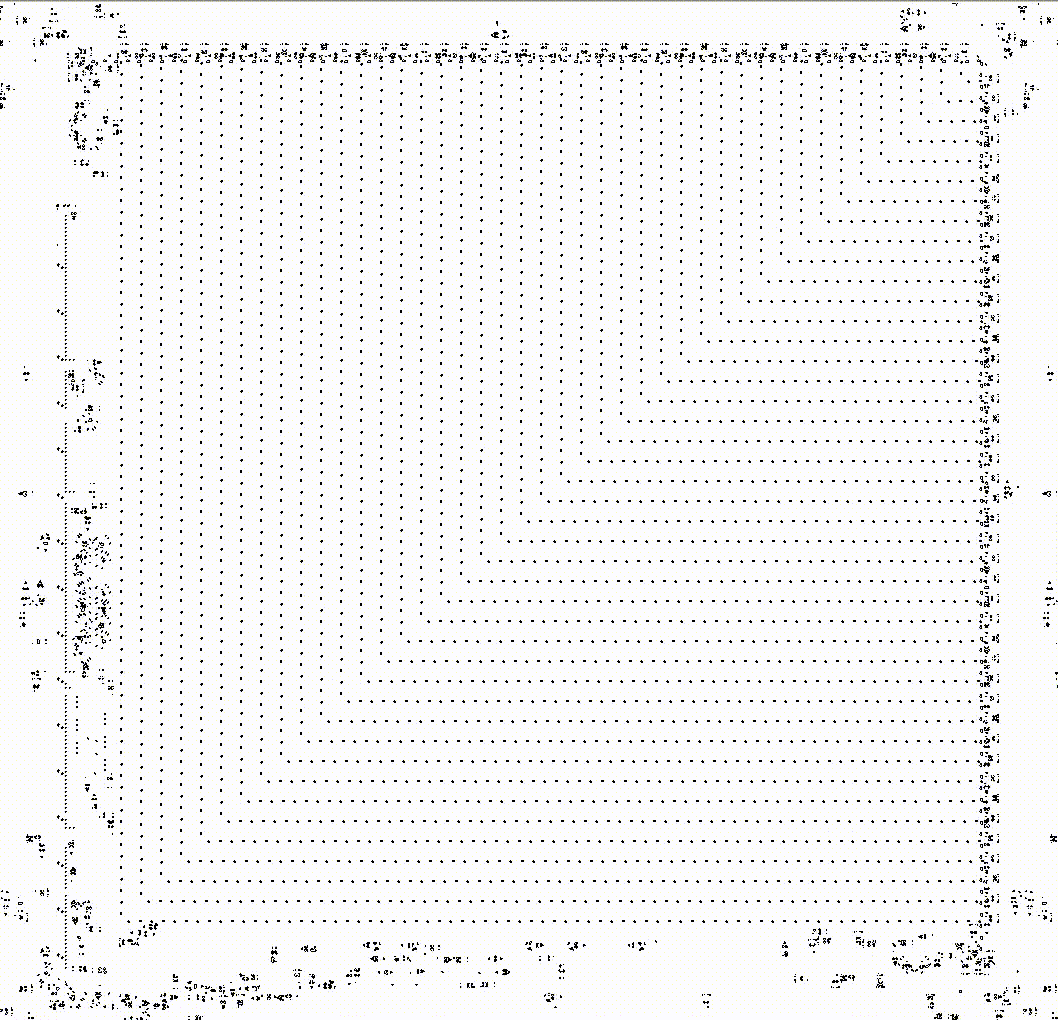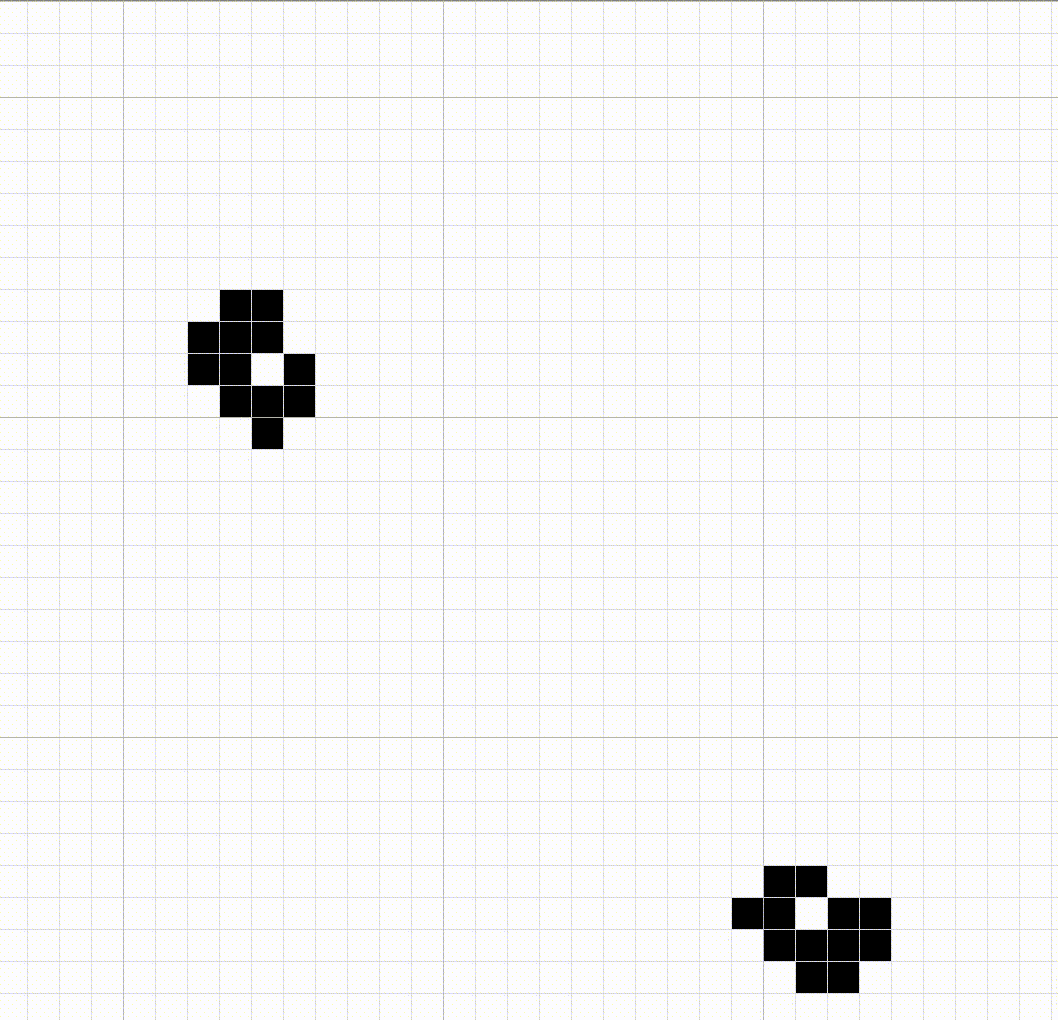
Любопытный читатель задастся вопросом: "А можно ли из метаклеток построить… метаклетку"? И ответ на этот вопрос, конечно, утвердительный. Ниже произведение инженерного искусства, демонстрирующее бесконечное поле игры жизнь, в котором сетка состоит из метаклеток. На этой сетке движутся паттерны, из которых состоят метаклетки на более высоком уровне, которые в свою очередь составляют сетку из метаклеток, по которой движутся паттерны, из которых на более высоком уровне состоят другие метклетки. И так далее.

Попробуйте самостоятельно поделать zoom in и zoom out в этой бесконечной игре, чтобы лучше понять как она устроена.
Аналогии
Мы видим бесконечную вселенную, которая работает на трех простых правилах. Нашему мозгу очень сложно вместить в себя бесконечность. Посмотрите ночью в небо и попробуйте представить расстояния до звезд, такие, что пока свет от звезды доходит до земли, звезда уже успевает сместиться на новое место в своем движении по галактике. Солнце было на том месте, которые мы видим 8 минут назад, а это самая близкая к нам звезда.
Нам кажется, что если долго долго делать zoom in, то рано или поздно достигнешь тех изначальных клеток, на которых построен первый уровень сетки из метаклеток. Мы привыкли к тому, что все вещи где-нибудь начинаются и где-нибудь заканчиваются. Если долго разбирать матрешку, то внутри будет самая маленькая матрешка, которая уже не разбирается. Но если поле по-настоящему бесконечно, то вы никогда не достигнете клеток из которых все состоит. Это бесконечная рекурсия, которая порождает сама себя. Каждый уровень основывается на предыдущем и создает следующий. И нет самого первого уровня и самого последнего.
Мы не видим бесконечных рекурсий вокруг. Всегда есть последний уровень, на котором рекурсия останавливается. Но что если конечность вещей - это только иллюзия? Условность, которая помогает нам думать о мире. Если посадить желудь в землю и из него вырастит дуб, то в какой момент желудь перестал быть желудем и стал ростком и в какой момент росток перестал быть ростком и стал деревом? Можем ли мы прочертить четкие границы?
В "Сутре сердца совершенной мудрости" (Prajñāpāramitā Hridaya Sūtra) сказано "Форма – пустотность, пустотность – форма. Форма не отдельна от пустотности, пустотность не отдельна от формы." И дальше "Нет глаза, нет уха, нет носа, нет языка, нет тела, нет ума". Я долго пытался понять, что буддисты имеют в виду, когда говорят о пустоте. Это что значит, что мир нам только кажется и ничего на самом деле нет?
Нам кажется, что мир состоит из изолированных вещей, которые существуют сами по себе. Вот дерево. Оно как бы существует само по себе. Но дерево не существует без земли, влаги, солнца. И оно никогда бы не появилось если бы не желудь из которого оно выросло. А для того, чтобы был желудь, нужно чтобы было дерево, с которого этот желудь упал. А значит для этого должна была появиться жизнь на земле и все эти условия из солнца, круговорота воды в природе, не слишком жаркого и не слишком сырого климата многие миллионы лет. Без всего этого дерева бы просто не было. И строго говоря оно не появилось, через желудь оно продолжение всех деревьев, что были до него. Это бесконечная трансформация в которой все связано со всем.
Математик Эдвард Лоренц, который работал над математической моделью глобального климата, ввел понятие "эффект бабочки". Термин, который возник из научной статьи, представленной им в 1972 году под названием: "Предсказуемость: вызывает ли взмах крыльев бабочки в Бразилии торнадо в Техасе?" Построив свою модель он обнаружил, что долгосрочный прогноз погоды необычайно чувствителен к малейшим возмущениям. Бабочка своим полетом может изменить состояние атмосферы и будущую погоду так же, как она повлияла на события, развертывающиеся в рассказе Брэдбери "И грянул гром".
Так связаны все клетки в игре жизнь. Изменение состояния любой клетки влечет за собой изменение состояния соседних, те в свою очередь меняют состояние своих соседей. Так каждая клетка связана с каждой клеткой на бесконечном поле. Стоит передвинуть одну клетку и получить "П" вместо "H" и система ведет себя совершенно по-другому. Все зависит ото всего.
И поскольку любой объект в мире состоит из частей, любой объект зависит от своих частей. Всё является частью чего-нибудь другого. Верхний уровень на нашем бесконечном поле Игры Жизнь составленном из метапикселей зависит от нижнего, потому что метаклетка состоит из клеток на более низком уровне. Так что все в мире - это временная совокупность частей, которая рано или поздно распадется, чтобы пересобраться в другую совокупность. Точно так же как включаясь и выключаясь клетки образуют паттерны, которые составляют матаклетки, образующие сетку на более высоком уровне, на этой сетке включаются и выключаются клетки, обзауя паттерны, которые составляют сетку для следующего уровня. Нет ничего что бы существовало изолированно и нет ничего что существовало бы вечно. Все что мы видим - только временная совокупность частей, как камешки подброшенные в воздух на мгновение складываются в некоторый рисунок.
Вот так, проводя аналогии, мы с помощью Игры Жизнь можем по-новому посмотреть на привычный нам мир. Увидеть, что дерево, бабочка, климат и, в целом, любой объект - это только паттерн, выхваченный нашим сознанием из бесконечной трансформации бесконечного количества атомов связанных друг с другом.
Из этого понимания можно сделать много выводов. Например, что я - это не изолированная личность никак не связанная с другими. Я - часть хоровода жизни, в котором все связаны со всеми. Все знания, деньги, любые другие ресурсы есть у меня благодаря другим людям. Вы читаете этот блог, потому что наши предки создали язык, на котором он написан, миллионы людей создавали огромное количество технологий, которые позволили мне этот блог сделать и доставить его до вас. В одном только этом процессе задействованы миллионы людей. В следующий раз, когда будете покупать банан в супермаркете подумайте сколько миллионов людей сделало это возможным. Мы все связаны. Поэтому, например, я могу быть счастлив сделав счастливым кого-то другого. Эта простая мысль может улучшить жизнь миллионов людей чувствующих себя одинокими. Тебе одиноко? Найди кого-нибудь кто так же одинок как ты и улыбнись ему, заведи с ним разговор. И вот вы уже оба не одиноки.
Аналогия не может быть доказательством чего-то. Тот факт, что две вещи похожи, еще ни о чем не говорит. Например, мозг по своей форме напоминает грецкий орех и вряд ли это может что-то значить. Но иногда аналогия помогает взглянуть на вещи по-новому. Из аналогии может родиться гипотеза. Если вещи похожи, то может они и работают одинаково? Гипотезу еще нужно проверить. Однако, наличие гипотезы - это уже большой шаг в продвижении к пониманию.
В Игре Жизнь мы видим бесконечную вселенную, которая работает на трех простых правилах. Кто знает, может быть и наша вселенная, несмотря на свое кажущееся многообразие, тоже построена на очень простых правилах. Например, закон сохранения энергии по которому энергия не возникает и не пропадает, а просто меняет формы, работает как на микро уроне, так и на макро уровне. Иллюстрацией этого может служить маятник. Когда маятник находится на самой верхней точке своего движения, его потенциальная энергия максимальна, а кинетическая равна нулю. Когда маятник движется, потенциальная энергия переходит в кинетическую, которая достигает максимума в нижней точке и потом уже кинетическая энергия начинает переходить в потенциальную. Точно так же электрон может переходить между различными энергетическими уровнями, что аналогично колебаниями маятника. Когда электрон находится на более высоком энергетическом уровне, у него есть больше потенциальной энергии. При переходе на более низкий уровень, электрон теряет потенциальную энергию, которая высвобождается в виде фотона. Как сказано в Изумрудной скрижали "То, что вверху, происходит от того, что внизу, а то, что внизу, происходит от того, что вверху". Надписи этой никак не меньше 1000 лет.
В какой-то момент детали важны
Математик Льюис Фрай Ричардсон исследовал влияние длины государственных границ на вероятность начала военных конфликтов и заметил следующее: Португалия заявила, что её сухопутная граница с Испанией равна 987 км, а Испания определила её равной 1 214 км. Как это может быть? Граница между странами одна и та же. Ричардсон обнаружил, что это ошибка округления, связанная с масштабированием. При увеличении масштаба мы начинаем рассматривать все более мелкие фрагменты границы, которые были не видны при более грубом масштабе. Эти мелкие фрагменты добавляют свою длину к общей длине границы, что приводит к ее увеличению. Чем больше масштаб измерения, тем длиннее измеряемая граница. Таким образом, испанские и португальские географы попросту руководствовались измерениями разных масштабов. Наиболее удивительно то, что при увеличении точности, длинна границы стремится к бесконечности.
Изучая проблему длины береговой линии Великобритании, Мандельброт заметил, что береговая линия состоит из чередования заливов и мысов.

Так Мандельброт и открыл фракталы. Свойством фракталов является самоподобие, заключающееся в проявлении одной и той же общей фигуры на любом масштабе. Независимо от того, насколько сильно масштабируется та или иная часть береговой линии, всё равно проявляется аналогичная картина меньших заливов и мысов, наложенная на бо́льшие заливы и мысы, вплоть до песчинок. Чем больше масштаб, тем больше заливов и мысов, тем длиннее береговая линия.

Длина береговой линии или границы стремящаяся к бесконечности - это детали, которыми люди пренебрегали на протяжении большей части своей истории. Удивительно, что до середины 20-ого века этого никто не замечал.
Борьбой со сложностью можно настолько увлечься, что перепутать абстракцию со сжатием без потерь. Или перепутать аналогию с абстракцией. Мы можем забыть, что нашей конечной целью является не построение стройной теории, а предсказание того как мир работает. Теория может быть очень красивой и стройной, но если нашлись детали, которые ей противоречат, их придется принять во внимание. В конечном итоге мы боремся с энтропией, а не со сложностью.
Абстракция в коммуникации
Почему важно понимать на каком уровне абстракции ты находишься? Построение абстракции включает в себя изучение деталей, выделение важных и отбрасывание несущественных. Очень часто мы предполагаем, что наш собеседник тоже знает все эти детали и понимает абстракцию, которую мы используем. Абстракции очень сокращают время, необходимое для передачи информации. Мы для этого их и создаем. Но часто ваше предположение неверно. Иногда нужно потратить время, чтобы спуститься на уровень ниже и проверить одинаково ли наше понимание деталей. Так нужно делать даже когда собеседник - это вы сам. Иногда кажется, что мы понимаем детали и поэтому можем безопасно использовать абстракцию. Но так ли это?
Тут, что я вынужден сказать, что демонстрация бесконечного поля Игры Жизнь, где каждая клетка рекурсивно состоит из бесконечного количества метаклеток, конечно же не настоящая Игра Жизнь. Это просто демонстрация. Вот тут автор описал как он ее сделал и это очень интересно для специалистов. Для не специалистов стоит сказать, что бесконечность - математическая конструкция. В реальной жизни ресурсы вычислительных мощностей (будь то ресурсы компьютера или человеческого мозга) ограничены. То как мы эту ограниченность преодолеваем в нашем стремлении к бесконечности и есть технический прогресс и личное развитие каждого человека.
Заключение
Сложность является универсальным феноменом, который присутствует во всех областях жизни, от науки и технологий до культуры и социальных систем. Процесс борьбы с энтропией, процесс изучения окружающего мира - это всегда процесс упрощения. Но можно упрощать просто избегая сложностей. А можно нырять в сложность с головой. Удивляться сюрпризам эмерджентности, выстраивать структуру из хаоса, передавать свои открытия другим, теряться в слоях абстракций, натыкаться на детали, которые рушат эти слои и возводить новые слои, проводить неожиданные аналогии и делать новые открытия. Красота фракталов и бесконечность над головой - мир прекрасен своей сложностью!
В книжке "Перегруженный мозг: Информационный поток и пределы рабочей памяти" Торкель Клингберг изучает как количеством информации, которую человек может временно хранить и манипулировать в уме влияет на когнитивные способности. Оказывается от количества объектов, которые человек может одновременно удерживать в рабочей памяти напрямую зависит его способность мыслить. Чем больше объектов убирается в рабочую память, тем мощнее мышление. Каждый раз когда вы сталкиваетесь со сложностью - это значит упираетесь в размер рабочей памяти. Объектов так много, что вы не можете за ними уследить. Хорошая новость в том, что рабочую память можно увеличивать, тренируя таким образом свою способность мыслить. Каждый раз преодолевая сложность, вы расширяете границы своей рабочей памяти и своего мышления. Не избегайте сложности! Наслаждайтесь ею!
